Solveeit Logo
Login

Question

Question: Find the distance between parallel lines $\frac{x}{2} = \frac{y}{-1} = \frac{z}{2}$ and $\frac{x-1}{...

Find the distance between parallel lines x2=y−1=z2\frac{x}{2} = \frac{y}{-1} = \frac{z}{2} and x−12=y−1−1=z−12\frac{x-1}{2} = \frac{y-1}{-1} = \frac{z-1}{2}

Answer

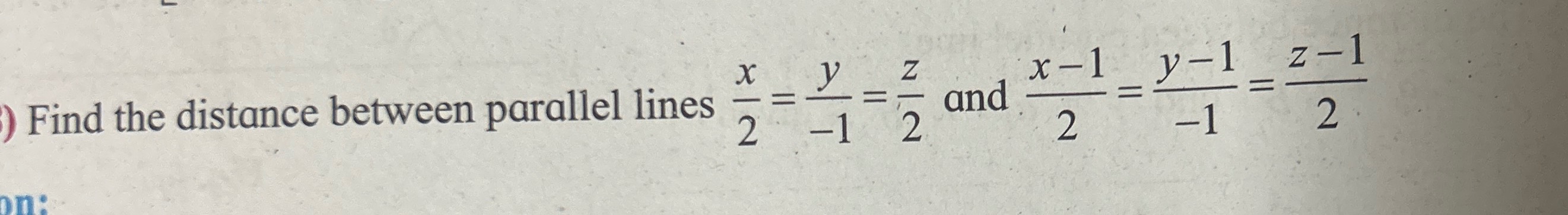
2\sqrt{2} units

Explanation

Solution

Solution Explanation:

  1. Write the parametric equations:
      For Line 1: Let t be a parameter, then
       x = 2t, y = –t, z = 2t.
      For Line 2: Let s be a parameter, then
       x = 1 + 2s, y = 1 – s, z = 1 + 2s.

  2. Choose one point from each line:
      - From Line 1 (for t = 0): A = (0, 0, 0)
      - From Line 2 (for s = 0): B = (1, 1, 1)

  3. The direction vector for both lines is d = (2, –1, 2).

  4. Calculate the vector AB = B – A = (1, 1, 1).

  5. Use the formula for the distance between parallel lines:
      Distance = |AB × d| / |d|.

  6. Compute the cross product:
      AB × d = (1, 1, 1) × (2, –1, 2)
      = ( (1×2 – 1×(–1)), –(1×2 – 1×2), (1×(–1) – 1×2) )
      = (2 + 1, –(2 – 2), (–1 – 2))
      = (3, 0, –3).

  7. Its magnitude is |AB × d| = √(3² + 0² + (–3)²) = √(9 + 9) = 3√2.

  8. Compute |d| = √(2² + (–1)² + 2²) = √(4 + 1 + 4) = 3.

  9. Therefore, the distance = (3√2) / 3 = √2.