Question

Find the current through CD in the given figure.

A. $I = \dfrac{{{R_3}\left( {{R_1} + {R_2}} \right) + {R_1}\left( {{R_3} + {R_4}} \right)}}{{{R_3}{R_4}\left( {{R_1} + {R_2}} \right) + {R_1}{R_2}\left( {{R_3} + {R_4}} \right)}}{V_0}$
B. $I = \dfrac{{{R_3}\left( {{R_1} + {R_2}} \right) - {R_1}\left( {{R_3} + {R_4}} \right)}}{{{R_3}{R_4}\left( {{R_1} + {R_2}} \right) + {R_1}{R_2}\left( {{R_3} + {R_4}} \right)}}{V_0}$
C. $I = \dfrac{{{R_3}\left( {{R_1} + {R_2}} \right) - {R_1}\left( {{R_3} + {R_4}} \right)}}{{{R_3}{R_4}\left( {{R_1} + {R_2}} \right) - {R_1}{R_2}\left( {{R_3} + {R_4}} \right)}}{V_0}$
D. Zero

Answer 1

Use Kirchoff’s junction rule, which states that the total current entering a junction is equal to total current flowing out through it, and assume some current through each wire.
Now, apply Kirchoff’s loop rule in the two bigger loops and one smaller loop and solve the three equations obtained to find the current through CD. The Kirchoff’s loop rule states that sum of potential difference across each resistors in a loop is zero. The potential drop across a resistance $R$ when current $I$ flows through it is given by $V = IR$ .

Complete step by step answer:
Let us first assume that current $I$ is drawn from the battery. Now we use the Kirchoff’s junction rule, which states that the total current entering a junction is equal to total current flowing out through it, to assume current through each wire.
Let current ${I_1}$ flow through ${R_1}$ then current $I - {I_1}$ will flow through ${R_3}$. Similarly ${I_2}$ flows through CD then currents through other resistors is given in the figure.

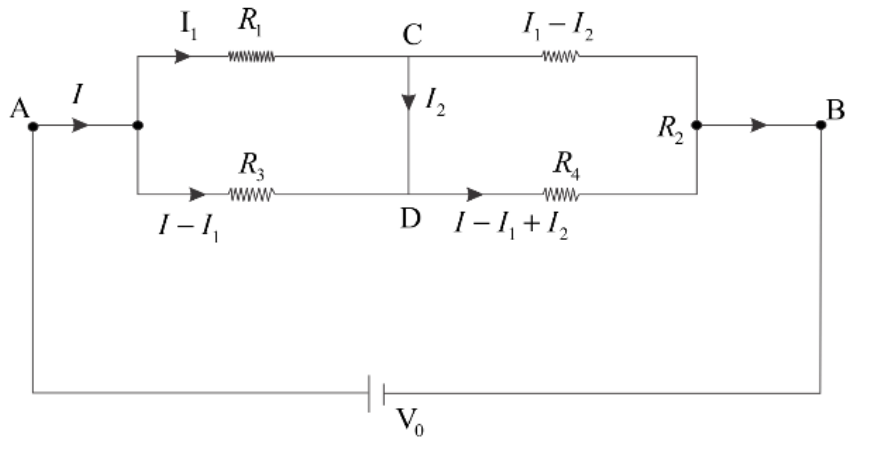
Now, we apply Kirchoff’s loop rule in the two bigger loops and one smaller loop and solve the three equations obtained to find the current through CD. The Kirchoff’s loop rule states that sum of potential difference across each resistors in a loop is zero. The potential drop across a resistance $R$ when current $I$ flows through it is given by $V = IR$ .
Applying Kirchoff’s loop rule in the small loop on the left hand side we have
${I_1}{R_1} = \left( {I - {I_1}} \right){R_3}$
On further solving we have
$I = \dfrac{{{I_1}\left( {{R_1} + {R_3}} \right)}}{{{R_3}}}$ ……(i)
Applying Kirchoff’s loop rule in the bigger loop containing ${R_1},{R_2}$ and the battery we have
${I_1}{R_1} + \left( {{I_1} - {I_2}} \right){R_2} = {V_0}$
On further solving we have
${I_1} = \dfrac{{{V_0} + {I_2}{R_2}}}{{{R_1} + {R_2}}}$ …..(ii)
Substituting the value of ${I_1}$ from equation (ii) in equation (i) we have
$I = \dfrac{{\left( {{V_0} + {I_2}{R_2}} \right)\left( {{R_1} + {R_3}} \right)}}{{\left( {{R_1} + {R_2}} \right){R_3}}}$ …..(iii)
Now, applying Kirchoff’s loop rule in the bigger loop containing ${R_3},{R_4}$ and the battery we have
$\left( {I - {I_1}} \right){R_3} + \left( {I - {I_1} + {I_2}} \right){R_4} = {V_0}$
Substituting the values of ${I_1}$ and $I$ from equations (ii) and (iii) we have
${I_2} = \dfrac{{{R_3}\left( {{R_1} + {R_2}} \right) - {R_1}\left( {{R_3} + {R_4}} \right)}}{{{R_3}{R_4}\left( {{R_1} + {R_2}} \right) + {R_1}{R_2}\left( {{R_3} + {R_4}} \right)}}{V_0}$ which is the current through CD.
Hence, option B is correct.

Note: While distributing the currents in different branches, try to limit the number of variables as much as you can. Increasing the variables means you have to solve more number of equations to get the final value.