Question

Find the current (in $A$) in the rightmost resistor shown in the figure

Answer 1

We will use a special method here which is just a manipulation of our idea that current flows from higher to lower potential. Through this, we will evaluate the value of the current flowing through the rightmost resistor in $A$.

Complete step by step answer:
Let us first mark the extreme upper left point as $0$ and as there is a vertical line from there without any external potential attached in between thus the extreme bottom left point can also be marked as $0$. These markings are just that these are our reference points where the potential is $0$.

Next as we go towards the right, the second upper left point can be marked as $- {\text{ }}2$. This is because, as we are flowing down the potential and moving from the extreme left to the second left, we come across an external potential of value $2{\text{ }}V$. Now, again the second bottom left can also be marked as $- {\text{ }}2$ for the same reason we did for the extreme left points.

Again, if we approach similarly, we can safely say that the second right points can be marked as $- {\text{ }}4$ and the extreme left points as $- {\text{ }}6$. The whole circuit after the process is shown in the following figure.

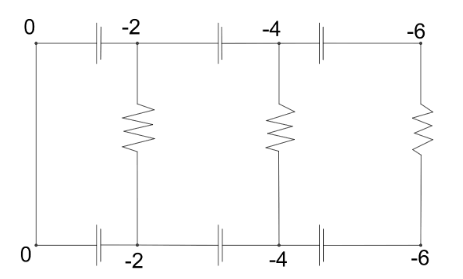
Now, clearly as the rightmost resistor lies between two points of equal potential, thus we can say that the potential difference across the resistor is zero and in turn there will be no current flowing through the resistor.

Hence, $0{\text{ }}A$ current flows through the rightmost resistor of the circuit.

Note: We can also say from the diagram that there will be no current flowing through any of the resistors for the same reason stated above. We can also arrive at this solution from our basic circuital knowledge. See, at the leftmost part, the two cells above and below are placed in opposite polarities and are of equal magnitude and thus the net current is zero. Coming towards the right, again the cells are placed with opposite polarities and same magnitude but this time the current from both the cells comes across a resistor but the resistor is the same for both and hence makes no difference and the net current flow here is also zero. Going with this approach, we can easily reach the result that the current flowing through the rightmost resistor is zero.