Question

Find the crystal field stabilization energy (CFSE) (in kJ/mol) for complex, ${\left[ {{\text{Ti}}{{\left( {{{\text{H}}_{\text{2}}}{\text{O}}} \right)}_6}} \right]^{3 + }}$. According to CFT, the first absorption maximum is obtained at $20,3000\,{\text{c}}{{\text{m}}^{ - 1}}$ for the transition.

Answer 1

Crystal field stabilization energy is defined as the energy of split orbital minus the energy of no-split orbitals. By using the relation of energy difference, and wavenumber calculate the energy from wavenumber. This energy will be equal to ${\Delta _{{\text{oh}}}}$ and multiply this energy with energy of electrons present in split d-orbitals of the metal.

Complete step by step answer:
The relation between energy and frequency is as follows:
$\Delta E\, = h\nu$
Where,
$\Delta E\,$ is the energy change.
$h$ is the Plank constant.
$\nu$ is the frequency.
The relation between frequency and wavelength is as follows:
$\nu = \dfrac{c}{\lambda }$
Where,
$c$ is the speed of light
$\lambda$is the Plank constant.
The relation between wavenumber and wavelength is as follows:
$\mathop \nu \limits^ - = \dfrac{1}{\lambda }$
Where,
$\mathop \nu \limits^ -$is the wavenumber.
So,
$\nu = c\mathop \nu \limits^ -$
Substitute the frequency value in energy formula as follows:
$\Delta E\, = hc\mathop \nu \limits^ -$
Substitute $6.6 \times {10^{ - 34}}{\text{J}}{\text{.s}}$ for Planck constant, $3 \times {10^{10}}{\text{cm}}{\text{.}}{{\text{s}}^{ - 1}}$for light speed and $20,3000\,{\text{c}}{{\text{m}}^{ - 1}}$ for wavenumber.
$\Rightarrow \Delta E\, = 6.6 \times {10^{ - 34}}{\text{J}}{\text{.s}} \times 3 \times {10^{10}}{\text{cm}}{\text{.}}{{\text{s}}^{ - 1}} \times 20,3000\,{\text{c}}{{\text{m}}^{ - 1}}$
$\Rightarrow \Delta E\, = 4.019 \times {10^{ - 18}}{\text{J}}$
So, the energy of one titanium ion is $4.019 \times {10^{ - 19}}{\text{J}}$.
Multiply the energy of one ion with Avogadro number to determine the energy of one mole.
Energy of one mole $= 4.019 \times {10^{ - 19}}{\text{kJ}}\, \times 6.02 \times {10^{23}}{\text{ion/mol}}$
$\Rightarrow = 241943\,{\text{J/mol}}$
Convert the energy value from joule to kilojoule as follows:
${\text{1000}}\,{\text{J}}\,{\text{ = 1 kJ}}$
$\Delta E\, = 242\,{\text{kJ/mol}}$
Valence electronic configuration of ${\text{T}}{{\text{i}}^{3 + }}$ is ${\text{3}}{{\text{d}}^1}$

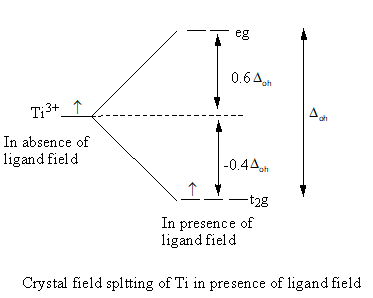
The energy of three, d-orbital decreases by $- 0.4{\Delta _{{\text{oh}}}}$ and energy of two, d-orbital increases by $0.6{\Delta _{{\text{oh}}}}$. The total energy change is equal to ${\Delta _{{\text{oh}}}}$.
So, the Crystal field stabilization energy of ${\left[ {{\text{Ti}}{{\left( {{{\text{H}}_{\text{2}}}{\text{O}}} \right)}_6}} \right]^{3 + }}$ is as follows:
The energy of one electron in split orbital is, $= 1 \times \left( { - \,0.4{\Delta _{{\text{oh}}}}} \right)$
$= - \,0.4{\Delta _{{\text{oh}}}}$
Substitute $242\,{\text{kJ/mol}}$ for ${\Delta _{{\text{oh}}}}$.
The energy of one electron in split orbital $= - \,0.4\, \times \,242\,{\text{kJ/mol}}$
The energy of one electron in split orbital $= - \,96.8\,\,{\text{kJ/mol}}$
So, the crystal field stabilization energy (CFSE) for the given complex is$- \,96.8\,\,{\text{kJ/mol}}$.

Note: The given ${\Delta _{{\text{oh}}}}$ is in the form of wavenumber, so it cannot be used directly. It should be converted into energy first. If the CFSE is asked into joule only then it is not required to multiply with Avogadro number.