Question
Question: Find the critical points of the function $y = \tan^{-1}(\sec x)$ where $x \in [-\frac{\pi}{2}, \frac...
Find the critical points of the function y=tan−1(secx) where x∈[−2π,2π]. Show your steps.
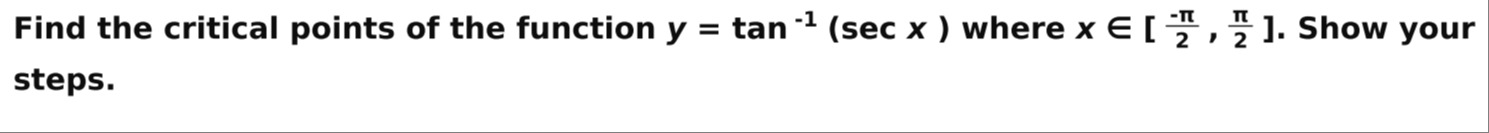
x=0
Solution
To find the critical points of a function y=f(x), we need to find the values of x in the domain of the function where either f′(x)=0 or f′(x) is undefined.
1. Determine the Domain of the Function: The given function is y=tan−1(secx). The domain of tan−1(u) is all real numbers, u∈(−∞,∞). The function secx=cosx1 is defined when cosx=0. In the interval x∈[−2π,2π], cosx=0 at x=−2π and x=2π. Therefore, the function y=tan−1(secx) is defined for x∈(−2π,2π). We will look for critical points within this open interval.
2. Calculate the First Derivative (y′): We use the chain rule for differentiation. Let u=secx. Then y=tan−1(u). The derivative of tan−1(u) with respect to u is 1+u21. The derivative of secx with respect to x is secxtanx. Applying the chain rule, y′=dudy⋅dxdu: y′=1+(secx)21⋅(secxtanx) y′=1+sec2xsecxtanx
3. Find Points where y′=0: Set the derivative equal to zero: 1+sec2xsecxtanx=0 The denominator 1+sec2x is always positive because sec2x≥1 for x∈(−2π,2π). Thus, 1+sec2x≥2, and it is never zero. Therefore, for y′ to be zero, the numerator must be zero: secxtanx=0 This implies either secx=0 or tanx=0.
- secx=0⟹cosx1=0, which is impossible for any real value of x.
- tanx=0. In the interval (−2π,2π), tanx=0 only when x=0.
So, x=0 is a critical point.
4. Find Points where y′ is Undefined: The derivative y′=1+sec2xsecxtanx would be undefined if:
- The denominator 1+sec2x=0. As established, this is never true.
- secx or tanx are undefined. Both secx and tanx are undefined at x=±2π. However, these points are outside the domain of the original function y=tan−1(secx). Within the domain (−2π,2π), secx and tanx are always defined, and thus y′ is always defined.
Therefore, there are no critical points where the derivative is undefined.
Conclusion: The only critical point of the function y=tan−1(secx) in the given interval is x=0.
