Question

Find the critical angle of the ray of light at glass water interface if the refractive indices of glass and water are 1.62 and 1.32 respectively.

Answer 1

The above stated problem is an easy application of the Snell’s law of refraction. Snell's law is a formula used when applied to light or other waves moving across a barrier between two distinct isotropic media, such as water, glass or air, to establish the relationship between the angles of incidence and refraction. If a certain critical point is achieved by the angle of incidence in water, the refracted ray lies around the boundary, having a 90-degree refraction angle. This angle of incidence is referred to as the critical angle; it is the greatest angle of incidence that can still be refracted.
Formula used:
For solving this question, we will be using the formula from Snell’s Law for refraction is
${{\mu }_{1}}\sin {{\theta }_{1}}={{\mu }_{2}}\sin {{\theta }_{2}}$

Complete answer:
Before we start solving the problem that has been stated to us above, let us take a look at all the parameters that have been given to us

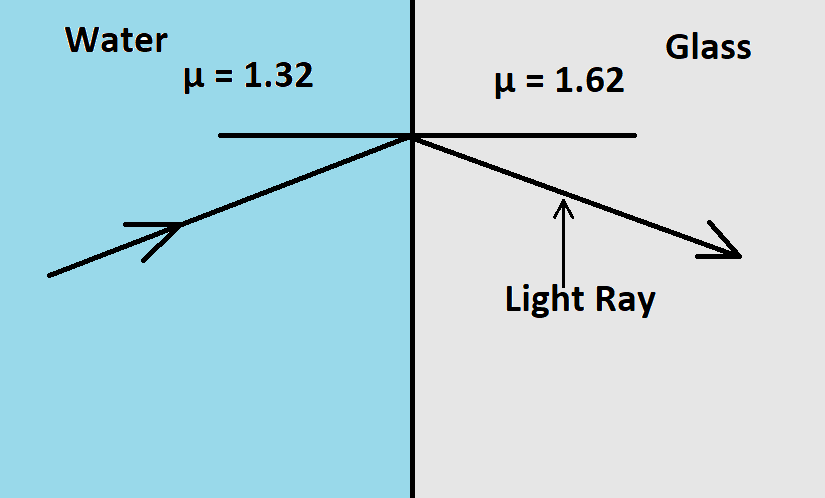
Let the refractive index of the glass be ${{\mu }_{1}}$
Then, ${{\mu }_{1}}$= 1.62
Also, let us assume the refractive index of the water to be ${{\mu }_{2}}$
Then, again
${{\mu }_{1}}$= 1.32
Now,
By applying the Snell’s law for refraction,
We have
${{\mu }_{1}}\sin {{\theta }_{1}}={{\mu }_{2}}\sin {{\theta }_{2}}$
Where ${{\theta }_{1}}$ and ${{\theta }_{2}}$ are the angle of incidence and angle of refraction
Now,
If the ray is going from water to glass,
Then, the critical angle will be
$\Rightarrow {{\theta }_{c}}={{\sin }^{-1}}(\dfrac{{{\mu }_{1}}}{{{\mu }_{2}}})$
So, now
By substituting the values we have in the above formula
We have
$\Rightarrow {{\theta }_{c}}=\sin (\dfrac{1.32}{1.62})$
$\Rightarrow {{\theta }_{c}}={{54.57}^{\circ }}$
So, the critical angle of the ray of light at glass water interface if the refractive indices of glass and water are 1.62 and 1.32 respectively will be ${{54.57}^{\circ }}$

Note:
If the ray of light was entering from glass to the water, then the critical angle will not exist as the ratio of the two refractive indices will be greater than 1, and sin function does not exist for a value greater than 1.