Question

Find the coordinates of the point which is three-fourth of the way from $A$ $\left( {3,1} \right)$ to $B$ $\left( { - 2,5} \right)$.

Answer 1

In the given question, we are required to find the coordinates of a point which divides the line segment joining the two given points. The required task can be done using the section formula where we find the coordinates of a point using a predefined formula given the coordinates of the end points of the line segment and the ratio in which the point divides the line segment. In the problem, we have to first calculate the ratio in which the line is divided by the point and then use the section formula to find the coordinates of the point.

Complete step by step answer:
We are given that the point divides the line segment joining the points and is three-fourth of the way from A $\left( {3,1} \right)$ and B $\left( { - 2,5} \right)$. Let us assume the required point to be P.
Hence, $AP = \dfrac{3}{4}\left( {AB} \right)$.
So, substituting $AB = AP + PB$, we get,
$P = \dfrac{3}{4}\left( {AP + PB} \right)$
$\Rightarrow 4AP = 3AP + 3PB$
Shifting the terms of the equation to find the ratio of the portions AP and PB, we get,
$AP = 3PB$
$\Rightarrow \dfrac{{AP}}{{PB}} = \dfrac{3}{1}$
So, the ratio of the portions AP and PB is $3:1$.

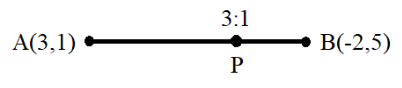
Now, we know the endpoints of the line segment $AB$ and the ratio in which the point $P$ divides the line segment $AB$. So, we can easily find out the coordinates of the point $P$ using the section formula. Using section formula, Coordinates of point $P = \left( {\dfrac{{n{x_1} + m{x_2}}}{{m + n}},\dfrac{{n{y_1} + m{y_2}}}{{m + n}}} \right)$, where $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are the coordinates of the endpoints of the line segment and $m:n$ is the ratio in which the Point $P$ divides the line segment.

$\text{Coordinates of Point P} = \left( {\dfrac{{1\left( 3 \right) + 3\left( { - 2} \right)}}{{3 + \left( { - 2} \right)}},\dfrac{{1\left( 1 \right) + 3\left( 5 \right)}}{{3 + \left( { - 2} \right)}}} \right)$
Opening the brackets and simplifying the calculations, we get,
$\text{Coordinates of Point P}= \left( {\dfrac{{3 - 6}}{1},\dfrac{{16}}{1}} \right)$
$\therefore \text{Coordinates of Point P}= \left( { - 3,16} \right)$

Hence, the coordinates of the point which is three-fourth of the way from A$\left( {3,1} \right)$ to B$\left( { - 2,5} \right)$ are $\left( { - 3,16} \right)$.

Note: We must remember the section formula and its applications in order to solve the problem. We should understand the language of the question carefully as without understanding the problem, one might not be able to solve it properly. We should know how to solve for the ratio in which a point divides the line segment in different innovative and analytical ways.