Solveeit Logo
Login

Question

Question: Find the coordinates of the point \(P\left( {2,4} \right)\) with respect to the translated axis with...

Find the coordinates of the point P(2,4)P\left( {2,4} \right) with respect to the translated axis with origin at (1,3)\left( {1,3} \right)
A. (1,−1)\left( {1, - 1} \right)
B. (1,1)\left( {1,1} \right)
C. (−1,−1)\left( { - 1, - 1} \right)
D. (−1,1)\left( { - 1,1} \right)

Explanation

Solution

We will first consider the random point P(x,y)P\left( {x,y} \right) and a fixed point O′(h,k)O'\left( {h,k} \right) in the X−YX - Y plane. As we know that the equations X=x−h,Y=y−kX = x - h,Y = y - k are called transformation equations and then convert the point P(x,y)P\left( {x,y} \right) with respect to the new coordinate systemP(x−h,y−k)P\left( {x - h,y - k} \right). As we are given the translated axis origin point so put it equal toO′(0+h,0+k)O'\left( {0 + h,0 + k} \right) to determine the values of hh and. Thus, we get the point P(x,y)P\left( {x,y} \right) and P(x−h,y−k)P\left( {x - h,y - k} \right) by substituting the values.

Complete step by step Answer:

Let P(x,y)P\left( {x,y} \right) be any point in the XYXYplane. Let O′(h,k)O'\left( {h,k} \right) be the fixed point in XYXYplane. We draw two perpendicular axes throughO′O'. The XX-axis is parallel to xx-axis and YY-axis is parallel to yy-axis. O′O'Is the new origin for XYXYplane. The point PP has the coordinates(X,Y)\left( {X,Y} \right) with respect to the XYXYplane.
Consider the diagram:

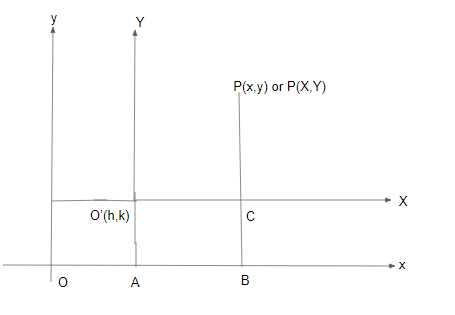
Thus the point P(x,y)P\left( {x,y} \right) with respect to the XYXYplane is P(x−h,y−k)P\left( {x - h,y - k} \right)
From the diagram and given in the question:
Translated axis origin is at O′(1,3)O'\left( {1,3} \right)
Now
The translated point is O′(0+h,0+k)O'\left( {0 + h,0 + k} \right)
Now we will put the translated axis origin and the translated point equal to determine the value of (h,k)\left( {h,k} \right)
Thus we get:
⇒O′(0+h,0+k)=O′(1,3) ⇒0+h=1 and 0+k=3 ⇒h=1 and k=3  \Rightarrow O'\left( {0 + h,0 + k} \right) = O'\left( {1,3} \right) \\\ \Rightarrow 0 + h = 1 \\\ and \\\ 0 + k = 3 \\\ \Rightarrow h = 1 \\\ and \\\ k = 3 \\\
Now from the given question, given (x,y)\left( {x,y} \right) points i.e. P(x,y)P\left( {x,y} \right), put these points in translated point equation i.e. O′(0+h,0+k)O'\left( {0 + h,0 + k} \right)
Where
h=1 and k=3  h = 1 \\\ and \\\ k = 3 \\\
This we get:
Translated points:
P′(2−1,3−4) ⇒P′(1,1)  P'\left( {2 - 1,3 - 4} \right) \\\ \Rightarrow P'\left( {1,1} \right) \\\
Thus we get the translated point as P′(1,1)P'\left( {1,1} \right).
The correct option is B.
Note: It’s necessary to construct the diagram for the given question. We have used the concept of transformation of the axis. As we have also found the new coordinate using the old coordinates. We have obtained the value of h and kh{\text{ and }}k to obtain the value of new coordinates.