Question

Find the coordinates of the point of trisection of the line segment joining the points $A\left( {7, - 2} \right)$ and $B\left( {1, - 5} \right)$

Answer 1

Here, we will assume two points such that they divide the given line segment in their respective ratios according to their position. We will use Section formula, to find the required coordinates of the point of trisection. Substituting the values of the given coordinates and the ratio in which the point divides the line segment in the section formula, we will get the required ratio.

Formula Used:
Section Formula: Coordinates of point$P = \dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}$, where $P$ is a point dividing the line segment.

Complete step-by-step answer:
The given coordinates of the end points of the line segment $AB$ are: $A\left( {7, - 2} \right)$ and $B\left( {1, - 5} \right)$
Now, in order to find the point of trisection, we have to divide this line segment into three parts.
Hence, let us assume two points $P$ and $Q$ on the line segment $AB$ such that:
Coordinates of point $P = \left( {x,y} \right)$ and Coordinates of point $Q = \left( {x\prime ,y\prime } \right)$
Hence, this line segment can be shown as:

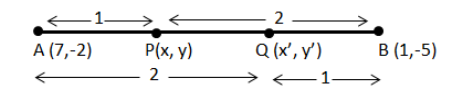
Now, point $P$ divides the line segment $AB$ in the ratio $1:2$ internally.
Also, $m$ and $n$ are the ratios in which the points have divided the line segment.
Now, substituting $\left( {{x_1},{y_1}} \right) = \left( {7, - 2} \right)$ , $\left( {{x_2},{y_2}} \right) = \left( {1, - 5} \right)$ and the ratio $m:n = 1:2$ in the formula Coordinates of Point $P = \dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}$, we get
Coordinates of point $P = \dfrac{{\left( 1 \right)\left( 1 \right) + 2\left( 7 \right)}}{{1 + 2}},\dfrac{{\left( 1 \right)\left( { - 5} \right) + 2\left( { - 2} \right)}}{{1 + 2}}$
Substituting coordinates of point $P = \left( {x,y} \right)$ in the above equation, we get
$\Rightarrow \left( {x,y} \right) = \dfrac{{1 + 14}}{3},\dfrac{{ - 5 - 4}}{3}$
Adding the terms in the numerator, we get
$\Rightarrow \left( {x,y} \right) = \dfrac{{15}}{3},\dfrac{{ - 9}}{3}$
Dividing the numerator by 3, we get
Hence, we get,
$\Rightarrow \left( {x,y} \right) = \left( {5, - 3} \right)$
Therefore, the coordinates of point $P$ are $\left( {5, - 3} \right)$
Now, similarly, point $Q$ divides the line segment $AB$ in the ratio $2:1$ internally.
Now, substituting $\left( {{x_1},{y_1}} \right) = \left( {7, - 2} \right)$ , $\left( {{x_2},{y_2}} \right) = \left( {1, - 5} \right)$ and the ratio $m:n = 2:1$ in the formula Coordinates of Point $Q = \dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}$, we get
Coordinates of point $Q = \dfrac{{\left( 2 \right)\left( 1 \right) + 1\left( 7 \right)}}{{2 + 1}},\dfrac{{\left( 2 \right)\left( { - 5} \right) + 1\left( { - 2} \right)}}{{2 + 1}}$
Substituting coordinates of point $Q = \left( {x\prime ,y\prime } \right)$ in the above equation, we get
$\Rightarrow \left( {x\prime ,y\prime } \right) = \dfrac{{2 + 7}}{3},\dfrac{{ - 10 - 2}}{3}$
Adding the terms in the numerator, we get
$\Rightarrow \left( {x\prime ,y\prime } \right) = \dfrac{9}{3},\dfrac{{ - 12}}{3}$
Dividing the numerator by 3, we get
$\Rightarrow \left( {x\prime ,y\prime } \right) = \left( {3, - 4} \right)$
Therefore, the coordinates of point $Q$ are $\left( {3, - 4} \right)$
Hence, the coordinates of the point of trisection of the line segment joining the points $A\left( {7, - 2} \right)$ and $B\left( {1, - 5} \right)$ are $\left( {5, - 3} \right)$ and $\left( {3, - 4} \right)$.
Hence, this is the required answer.

Note: In this question, the end points are given with their respective coordinates. We should take care while solving the question, that we substituted the correct coordinates in the correct place. For example, in the section formula, if we substitute $\left( {{x_1},{y_1}} \right)$ in such a way that the $x$ coordinate is of point $A$ and the $y$ coordinate is of point $B$. Then, our answer will be wrong. Also, while substituting the ratio in case of point $P$and $Q$ respectively, we should know that $1:2$ is different from $2:1$, hence, we should substitute the ratio carefully and accordingly.