Question

Find the coordinates of the orthocentre of the triangles whose angular points are
$(1,0)$,$(2, - 4)$ and $( - 5, - 2)$ .

Answer 1

Hint: First of all, draw the diagram and assume given points as A,B and C .Through point A draw a perpendicular line to BC and through point C draw a perpendicular line to AB.Find the slope of AD and EC with help of slope of lines AB and BC.After finding the slopes write an equations for lines AD and EC , intersection of these lines AD and EC at point we get required Orthocentre of triangle.

Complete step-by-step answer:
Let us assume the given points such that
$A( - 5, - 2)$ ,$B(1,0)$ and $C(2, - 4)$

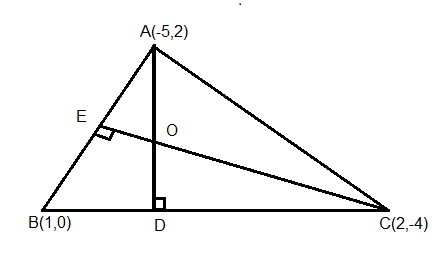
Now we know that the slope
${m_{}} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
Therefore, the slope of $AB$ is
$\;{m_{AB}} = \dfrac{{0 - ( - 2)}}{{1 - ( - 5)}} = \dfrac{1}{3}$ … (1)
Now, draw $CE$ perpendicular to $AB$
And we know that the product of slopes of perpendicular lines is $- 1$
$\therefore {m_{AB}}{m_{CE}} = - 1$
$\Rightarrow {m_{AB}} = \dfrac{{ - 1}}{{{m_{CE}}}}$
Now using the equation (1), we get
$\Rightarrow \dfrac{{ - 1}}{{{m_{CE}}}}{\text{ }} = {\text{ }}\dfrac{1}{3}$
$\dfrac{1}{3}{m_{CE}} = - 1$
$\Rightarrow {m_{CE}} = - 3$
Now, the equation of line can be given as
$y - {y_1} = m(x - {x_1})$
Therefore, the equation of $CE$ can be given as
$y + 4 = - 3(x - 2)$
$y + 4 = - 3x + 6$
$y + 3x = 6 - 4$
$y + 3x = 2$ … (2)
Now we know that the slope
${m_{}} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
Therefore, the slope of $BC$ is given as
$\; \Rightarrow {m_{BC}} = \dfrac{{ - 4 - 0}}{{2 - 1}} = - 4$ … (3)
Now draw $AD$ perpendicular to $BC$
${m_{BC}}{m_{AD}} = - 1$
$\; \Rightarrow {m_{BC}} = \dfrac{{ - 1}}{{{m_{AD}}}}$
Now, putting this value in equation (3)
$\; \Rightarrow \dfrac{{ - 1}}{{{m_{AD}}}} = - 4\;$
$- 4{m_{AD}} = - 1$
${m_{AD}} = \dfrac{1}{4}$
Now, the equation of $AD$ can be given as
$y + 2 = \dfrac{1}{4}(x + 5)$
$4y + 8 = x + 5$
$x - 4y = 3$ … (4)
The orthocentre is the point of intersection of perpendicular from opposite vertices. So, it is the point of intersection of $AD$ and $CE$
Now solving equation (2) and (4),
$y + 3x = 2$ … (2)
$x - 4y = 3$ … (4)
Now, multiplying equation (2) by 4, we get
$4(y + 3x) = 4(2)$
$4y + 12x = 8$ …. (5)
Adding equation (4) and (5), we get
$x + 12x - 4y + 4y = 3 + 8$
$13x = 11$
$\therefore x = \dfrac{{11}}{{13}}$
Putting this value in equation (4), we get
$\dfrac{{11}}{{13}} - 4y = 3$
$- 4y = 3 - \dfrac{{11}}{{13}}$
$- 4y = \dfrac{{39 - 11}}{{13}}$
$y = \dfrac{{28}}{{13 \times ( - 4)}}$
$\therefore y = \dfrac{{ - 7}}{{13}}$
So, the orthocentre of the triangle is $\left( {\dfrac{{11}}{{13}},\dfrac{{ - 7}}{{13}}} \right)$.

Note: To solve these types of questions, an adequate knowledge about the equations of line and slope is required. Using which, the required solution can be obtained.Students should remember the important formulas of finding the equation of line if two points are given and conditions of product of slopes if two lines are perpendicular.