Question

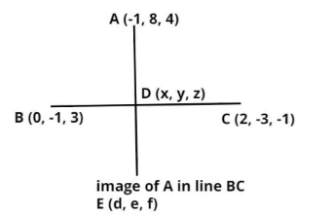
Find the coordinates of the foot of the perpendicular drawn from the point A (-1, 8, 4) to the line joining the points B (0, -1, 3) and C (2, -3, -1). Hence, find the image of the point A in the line BC.

Answer 1

Hint – IN this particular question use the concept that direction ratios of the line joining any points is the difference of the second point to the first point and the equation of the line joining these points is given as $\dfrac{{x - {x_1}}}{p} = \dfrac{{y - {y_1}}}{q} = \dfrac{{z - {z_1}}}{r}$, where, $\left( {{x_1},{y_1},{z_1}} \right)$ are the points of any end point of the line and (p, q, r) are the direction ratios so use these concepts to reach the solution of the question.

Complete step-by-step answer:
__
The direction ratios of the line joining B and C is the difference of the points C and the point B.
So the direction ratios of the line joining B and C are (2 – 0), (-3 – (-1)), (-1 – 3) which gives us (2, -2, -4).
Now the equation of the line joining points B and C is given as,
$\Rightarrow \dfrac{{x - {x_1}}}{p} = \dfrac{{y - {y_1}}}{q} = \dfrac{{z - {z_1}}}{r}$
Where, $\left( {{x_1},{y_1},{z_1}} \right)$ are the points of either point B or point C.
And (p, q, r) are the direction ratios.
So consider the points of B therefore,
The equation of the line joining points B and C is given as,
$\Rightarrow \dfrac{{x - 0}}{2} = \dfrac{{y - \left( { - 1} \right)}}{{ - 2}} = \dfrac{{z - 3}}{{ - 4}}$
$\Rightarrow \dfrac{{x - 0}}{2} = \dfrac{{y + 1}}{{ - 2}} = \dfrac{{z - 3}}{{ - 4}}$
Now let the foot of the perpendicular from the point A (-1, 8, 4) on the line BC be D (x, y, z).
Where (x, y, z) are the variable times the direction cosines of line BC and the sum of the point B.
Let the variable be m, where m is any real number.
Therefore, x = 2m, y = -2m + (-1) = -2m - 1 and z = -4m + 3.
Now the direction ratios of the line passing from point A and the foot of perpendicular on the line BC is
Let the direction ratios be (t, u, v).
So, t = (-1 – 2m), u = (8 – (-2m – 1)) = (9 + 2m) and v = (4 – (-4m + 3)) = (4m + 1)
Now the product of direction ratios of line BC and the direction ratios of the foot of the perpendicular line is always zero so we have,
$\Rightarrow pt + qu + rv = 0$
Now substitute the values we have,
$\Rightarrow 2\left( { - 1 - 2m} \right) - 2\left( {9 + 2m} \right) - 4\left( {4m + 1} \right) = 0$
Now simplify this we have,
$\Rightarrow \left( { - 2 - 4m} \right) - \left( {18 + 4m} \right) - \left( {16m + 4} \right) = 0$
$\Rightarrow - 24m - 24 = 0$
$\Rightarrow m = \dfrac{{24}}{{ - 24}} = - 1$
So the point D (x, y, z) is
x = 2(-1) = -2, y = -2(-1) – 1 = 1 and z = -4(-1) + 3 = 7.
Therefore, D = (-2, 1, 7)
Let the points of the image of point A in the line BC be E whose coordinates are (d, e, f).
So D is the midpoint of the points A and E.
So according to midpoint formula the coordinates of D are
$D = \dfrac{{A + E}}{2}$
Now D = (-2, 1, 7), A = (-1, 8, 4) and E = (d, e, f)
Therefore,
$- 2 = \dfrac{{ - 1 + d}}{2},1 = \dfrac{{8 + e}}{2},7 = \dfrac{{4 + f}}{2}$
Now simplify this we have,
$- 4 + 1 = d,2 - 8 = e,14 - 4 = f$
$d = - 3,e = - 6,f = 10$
So the image of the point A in the line BC is (-3, -6, 10)
So this is the required answer.

Note – Whenever we face such types of questions the key concept we have to remember is that the coordinates of the foot of the perpendicular in line BC are the variable (say m) times the direction cosines of line BC and the sum of the point B, so first find out the direction cosines of line BC then find out the coordinates of the foot of perpendicular on line BC then find out the direction cosines of this perpendicular line then multiplication of the direction cosines is always zero so from this calculate the value of m and hence calculate the point D (i.e. foot of the perpendicular) as above, then apply mid-point theorem and evaluate the coordinates of the image of the point A in line BC as above, we will get the required answer.