Question

Find the coordinates of the foot of the perpendicular drawn from the point $\left( {2,3} \right)$ to the line $3x - 4y + 7 = 0$?

Answer 1

Using the slope intercept form we will find the slope of the given line. Then as we know, when two lines are perpendicular then the product of their slope is equal to $- 1$. Using this we will find the slope of the line perpendicular to $3x - 4y + 7 = 0$. With the help of the given point $\left( {2,3} \right)$ and slope of the perpendicular line, we will find the equation of the line perpendicular to the given line $3x - 4y + 7 = 0$. Then we will find the point of intersection of these two lines which will give us the coordinates of the foot of the perpendicular.

Complete step by step answer:
Consider the figure below, let $AB$ be the given line $3x - 4y + 7 = 0$ and $CD$ be the line perpendicular to it. We have to find the foot of the perpendicular i.e., coordinate of point $D$.

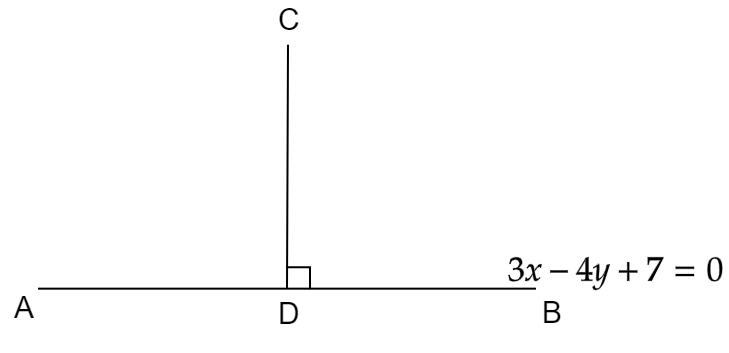
The slope intercept of the line is $y = mx + c$, where $m$ is the slope of the line.
Now, we have
$\Rightarrow 3x - 4y + 7 = 0$
On rewriting, we get
$\Rightarrow 4y = 3x + 7$
Dividing both the sides by $4$, we get
$\Rightarrow y = \dfrac{3}{4}x + \dfrac{7}{4} - - - (1)$
Therefore, on comparing with the slope intercept of a line, we get the slope of $AB$ as $\dfrac{3}{4}$.
Let the slope of the line $AB$ be ${m_1}$ and the slope of $CD$ be ${m_2}$.
So, we get ${m_1} = \dfrac{3}{4}$.
Now, the lines $AB$ and $CD$ are perpendicular. Therefore, ${m_1} \times {m_2} = - 1$.
We have,
$\Rightarrow {m_1} \times {m_2} = - 1$
Putting the value of ${m_1}$, we get
$\Rightarrow \dfrac{3}{4} \times {m_2} = - 1$
Multiplying both the sides by $\dfrac{4}{3}$, we get
$\Rightarrow {m_2} = - 1 \times \dfrac{4}{3}$
$\Rightarrow {m_2} = - \dfrac{4}{3}$
As we know that equation of a line passing through $\left( {{x_1},{y_1}} \right)$ and having slope $m$ is given by $y - {y_1} = m\left( {x - {x_1}} \right)$.
We get the equation of the line passing through $\left( {2,3} \right)$ and having slope $\left( { - \dfrac{4}{3}} \right)$ as:
$\Rightarrow y - 3 = - \dfrac{4}{3}\left( {x - 2} \right)$
On cross multiplication, we get
$\Rightarrow 3\left( {y - 3} \right) = - 4\left( {x - 2} \right)$
$\Rightarrow 3y - 9 = - 4x + 8$
On simplification, we get
$\Rightarrow 4x + 3y - 9 - 8 = 0$
$\Rightarrow 4x + 3y - 17 = 0 - - - (2)$
Now to find the coordinates of the foot of the perpendicular, we have to find the intersection of lines $AB$ and $CD$.
Putting $(1)$ in $(2)$, we get
$\Rightarrow 4x + 3\left( {\dfrac{3}{4}x + \dfrac{7}{4}} \right) - 17 = 0$
On taking the LCM, we have
$\Rightarrow \dfrac{{16x + 3\left( {3x + 7} \right) - 68}}{4} = 0$
On cross multiplication, we get
$\Rightarrow 16x + 3\left( {3x + 7} \right) - 68 = 0$
$\Rightarrow 16x + 9x + 21 - 68 = 0$
On simplification, we get
$\Rightarrow 25x - 47 = 0$
Adding $47$ both the sides, we get
$\Rightarrow 25x = 47$
Dividing both the sides by $25$, we get
$\Rightarrow x = \dfrac{{47}}{{25}}$
Putting the value of $x$ in $(1)$, we get
$\Rightarrow y = \left( {\dfrac{3}{4} \times \dfrac{{47}}{{25}}} \right) + \dfrac{7}{4}$
$\Rightarrow y = \dfrac{{141}}{{100}} + \dfrac{7}{4}$
Taking LCM, we get
$\Rightarrow y = \dfrac{{141 + 175}}{{100}}$
$\Rightarrow y = \dfrac{{316}}{{100}}$
On simplification, we get
$\Rightarrow y = \dfrac{{79}}{{25}}$
Hence, we get the coordinates of point $D$ as $\left( {\dfrac{{47}}{{25}},\dfrac{{79}}{{25}}} \right)$.
Therefore, the coordinates of the foot of the perpendicular drawn from the point $\left( {2,3} \right)$ to the line $3x - 4y + 7 = 0$ is $\left( {\dfrac{{47}}{{25}},\dfrac{{79}}{{25}}} \right)$.

Note:
The most important concept to solve this problem is to know that the product of slopes of two perpendicular lines is equal to $- 1$. In other words, perpendicular slopes are negative reciprocals of each other. Also note that, slopes of parallel lines are equal and the lines have different y-intercepts.