Solveeit Logo
Login

Question

Question: Find the coordinates of the foot of the perpendicular drawn from the origin to the plane \(2x - 3y +...

Find the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x−3y+4z−6=02x - 3y + 4z - 6 = 0

Explanation

Solution

We will let the coordinates of foot of perpendicular be (x1,y1,z1)\left( {{x_1},{y_1},{z_1}} \right). Let the normal vector to the place be n→=2i^−3j^+4k^\overrightarrow n = 2\hat i - 3\hat j + 4\hat k. We will calculate the direction ratios of both the vectors and will use it to find the value of coordinates in terms of a constant , say kk. We will then substitute it in the equation of the plane and find the value of kk. We can then substitute the value of kk to find the coordinates.

Complete step-by-step answer:
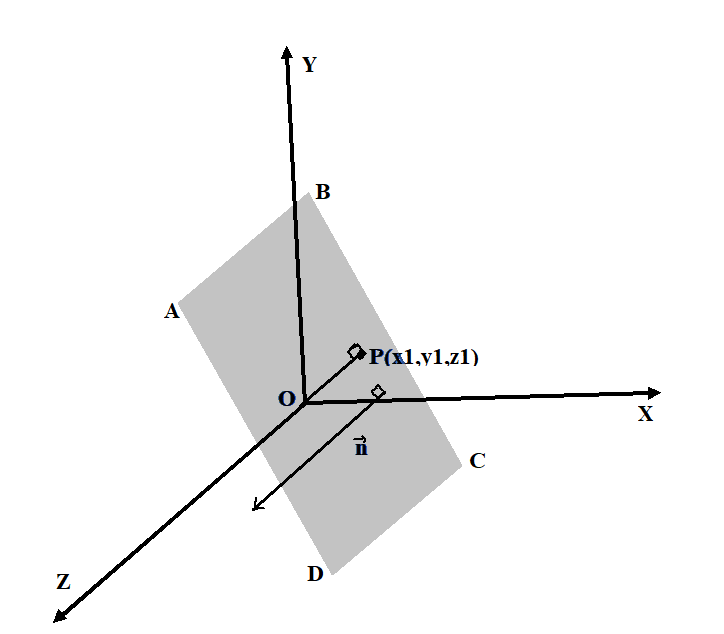
Let the coordinates of the foot of perpendicular be (x1,y1,z1)\left( {{x_1},{y_1},{z_1}} \right).
Now, perpendicular to the plane is parallel to the normal vector of the plane.
We are given that the equation of the plane is 2x−3y+4z−6=02x - 3y + 4z - 6 = 0
We can also write it as 2x−3y+4z=62x - 3y + 4z = 6
Then, the corresponding normal vector is n→=2i^−3j^+4k^\overrightarrow n = 2\hat i - 3\hat j + 4\hat k
This vector will be parallel to the vector OP→\overrightarrow {OP} which is the foot of perpendicular from origin to the plane 2x−3y+4z−6=02x - 3y + 4z - 6 = 0.

If two vectors are parallel, their direction ratios are proportional.
Direction ratio of OP→\overrightarrow {OP} are x1−0=x1{x_1} - 0 = {x_1}, y1−0=y1{y_1} - 0 = {y_1} and z1−0=z1{z_1} - 0 = {z_1}
And the direction ratio of normal vector is 2,−3,42, - 3,4
Then,
x12=y1−3=z14=k x1=2k,y1=−3k,z1=4k  \dfrac{{{x_1}}}{2} = \dfrac{{{y_1}}}{{ - 3}} = \dfrac{{{z_1}}}{4} = k \\\ {x_1} = 2k,{y_1} = - 3k,{z_1} = 4k \\\
We will now substitute the value of (x1,y1,z1)\left( {{x_1},{y_1},{z_1}} \right) in the equation of the plane to find the value of kk
2(2k)−3(−3k)+4(4k)−6=0 ⇒4k+9k+16k=6 ⇒29k=6 ⇒k=629  2\left( {2k} \right) - 3\left( { - 3k} \right) + 4\left( {4k} \right) - 6 = 0 \\\ \Rightarrow 4k + 9k + 16k = 6 \\\ \Rightarrow 29k = 6 \\\ \Rightarrow k = \dfrac{6}{{29}} \\\
Now, we will substitute the value of kk to find the value of coordinates of the foot of perpendicular.
x1=2(629)=1229 y1=−3(629)=−1829 z1=4(629)=2429  {x_1} = 2\left( {\dfrac{6}{{29}}} \right) = \dfrac{{12}}{{29}} \\\ {y_1} = - 3\left( {\dfrac{6}{{29}}} \right) = - \dfrac{{18}}{{29}} \\\ {z_1} = 4\left( {\dfrac{6}{{29}}} \right) = \dfrac{{24}}{{29}} \\\
Hence, the coordinates of the foot of perpendicular is (1229,−1829,2429)\left( {\dfrac{{12}}{{29}}, - \dfrac{{18}}{{29}},\dfrac{{24}}{{29}}} \right).

Note: Position vectors denote the location of a point from the origin. Also, perpendicular to the plane is parallel to the normal vector of the plane. The direction ratios of the two parallel vectors are proportional.