Question

Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for ${{x}^{2}}=-9y$ .

Answer 1

We recall the definition of directrix, focus and latus rectum. We compare the given equation of parabola with standard equation of parabola opening downward with vertex $\left( h,k \right)$ as ${{\left( x-h \right)}^{2}}=-4a\left( y-k \right)$ and find the vertex and $a$ . We use the formula for directrix $y=a$ , the coordinates of focus $F\left( 0,-a \right)$ and length of latus rectum $4a$ to obtain the required.

Complete step-by-step answer:
We know that when a point moves such that its distance from a fixed point is equal to its distance from a fixed line, then its locus is called parabola, the fixed line is called directrix and the fixed point is called the focus. The line perpendicular to the directrix and passing through the focus is called the axis of the parabola. The point of intersection of the axis and the parabola is called vertex. The line segment perpendicular to axis through the focus and with endpoints on the parabola is called latus rectum.$$$$

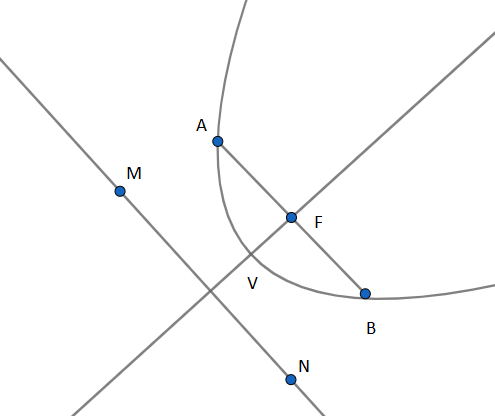
We have shown in the above figure of a parabola with the directrix MN, the vertex V, the focus F, the latus rectum AB. $$$$
We know that the standard equation of a parabola opens downward towards negative $y-$ axis with vertex $V\left( h,k \right)$ is given by the equation
${{\left( x-h \right)}^{2}}=-4a\left( y-k \right)..\left( 1 \right)$
We know that the equation of directrix of the parabola (1) is given by
$y=a$
The coordinates of the focus given by $F\left( 0,-a \right)$ and the length of the latus rectum is $4a$ . The equation parabola given in the question is
${{x}^{2}}=-9y...\left( 2 \right)$
We see that the above parabola is in the form of ${{x}^{2}}=-4ay$ and so the parabola (2) is a downward parabola. We compare equation of parabola (2) with equation of parabola (1) and have,
${{\left( x-0 \right)}^{2}}=-4\times \dfrac{9}{4}\times \left( y-0 \right)$
So we have vertex $V\left( 0,0 \right)$ and $a=\dfrac{9}{4}$ . So the equation of the directrix is

& y=a \\\ & \Rightarrow y=\dfrac{9}{4} \\\ \end{aligned}$$ The coordinates of the focus given by $ F\left( 0,-a \right)=F\left( 0,\dfrac{-9}{4} \right) $ and the length of the latus rectum is $ 4a=4\times \dfrac{9}{4}=9 $ . We plot the given parabola. $$$$  **Note:** The equations of the parabolas opened towards left, upward, right are given by $ {{y}^{2}}=4ax $ , $ {{x}^{2}}=4ay $ , $ {{y}^{2}}=-4ax $ respectively with corresponding of equations of directrices $ x=a,y=-a,x=-a $ , coordinates of foci as $ \left( a,0 \right),\left( 0,a \right),\left( -a,0 \right) $ and length of latus rectum for all parabola is $ 4a $ .