Solveeit Logo
Login

Question

Question: Find the coordinates of the circumcentre of the triangle whose vertices are (8,6) , (8,2) and (2,2)....

Find the coordinates of the circumcentre of the triangle whose vertices are (8,6) , (8,2) and (2,2). Also find its circumradius.

Explanation

Solution

The circumcenter of a triangle is defined as the point where the perpendicular bisectors of the sides of that particular triangle intersect. The circumcenter is also the centre of the circumcircle of that triangle. The radius of the circumcircle is the circumradius.
Since the radii of the circle are congruent, a circumcenter is equidistant from vertices of the triangle.

Complete step by step answer:

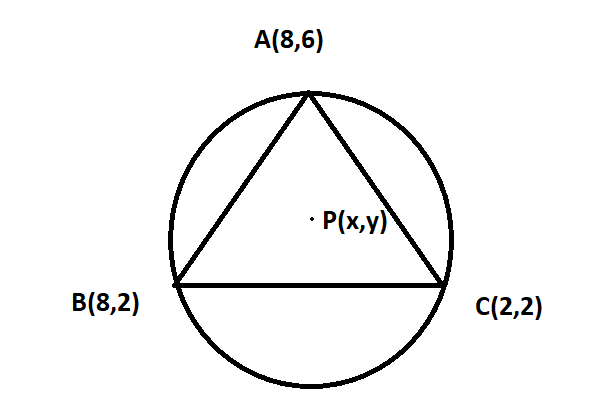
Let the three vertices of triangle A(8,6) B(8,2) C(2,2)
Let the circumcenter be P(x,y)
We now know that P is equidistant from A, B and C.
PA=PB=PC
(PA)2=(PB)2=(PC)2{{\left( PA \right)}^{2}}={{\left( PB \right)}^{2}}={{\left( PC \right)}^{2}}
The distance between two points (x1,y1)and(x2,y2)({{x}_{1}},{{y}_{1}})and({{x}_{2}},{{y}_{2}}) is (x1−x2)2+(y1−y2)2\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}
PA = (x−8)2+(y−6)2\sqrt{{{\left( x-8 \right)}^{2}}+{{\left( y-6 \right)}^{2}}}, (PA)2=(x−8)2+(y−6)2{{\left( PA \right)}^{2}}={{\left( x-8 \right)}^{2}}+{{\left( y-6 \right)}^{2}}
PB = (x−8)2+(y−2)2\sqrt{{{\left( x-8 \right)}^{2}}+{{\left( y-2 \right)}^{2}}}, (PB)2=(x−8)2+(y−2)2{{\left( PB \right)}^{2}}={{\left( x-8 \right)}^{2}}+{{\left( y-2 \right)}^{2}}
PC = (x−2)2+(y−2)2\sqrt{{{\left( x-2 \right)}^{2}}+{{\left( y-2 \right)}^{2}}}, (PB)2=(x−2)2+(y−2)2{{\left( PB \right)}^{2}}={{\left( x-2 \right)}^{2}}+{{\left( y-2 \right)}^{2}}
(PA)2=(PB)2{{\left( PA \right)}^{2}}={{\left( PB \right)}^{2}}
⇒(x−8)2+(y−6)2=(x−8)2+(y−2)2 ⇒x2+64−16x+y2+36−12y=x2+64−16x+y2+4−4y ⇒36−12y=4−4y ⇒8y=32 ⇒y=4 \begin{aligned} & \Rightarrow {{\left( x-8 \right)}^{2}}+{{\left( y-6 \right)}^{2}}={{\left( x-8 \right)}^{2}}+{{\left( y-2 \right)}^{2}} \\\ & \Rightarrow {{x}^{2}}+64-16x+{{y}^{2}}+36-12y={{x}^{2}}+64-16x+{{y}^{2}}+4-4y \\\ & \Rightarrow 36-12y=4-4y \\\ & \Rightarrow 8y=32 \\\ & \Rightarrow y=4 \\\ \end{aligned}

(PC)2=(PB)2{{\left( PC \right)}^{2}}={{\left( PB \right)}^{2}}
⇒(x−2)2+(y−2)2=(x−8)2+(y−2)2 ⇒x2+4−4x+y2+4−4y=x2+64−16x+y2+4−4y ⇒8−4x−4y=68−16x−4y ⇒68−8=16x−4x ⇒12x=60 ⇒x=5 \begin{aligned} & \Rightarrow {{\left( x-2 \right)}^{2}}+{{\left( y-2 \right)}^{2}}={{\left( x-8 \right)}^{2}}+{{\left( y-2 \right)}^{2}} \\\ & \Rightarrow {{x}^{2}}+4-4x+{{y}^{2}}+4-4y={{x}^{2}}+64-16x+{{y}^{2}}+4-4y \\\ & \Rightarrow 8-4x-4y=68-16x-4y \\\ & \Rightarrow 68-8=16x-4x \\\ & \Rightarrow 12x=60 \\\ & \Rightarrow x=5 \\\ \end{aligned}
Therefore the circumcenter is P(x,y) = (4,5)
Circumradius is PA=PB=PC
Substituting the values of x and y in PA = (x−8)2+(y−6)2\sqrt{{{\left( x-8 \right)}^{2}}+{{\left( y-6 \right)}^{2}}},
⇒PA=(4−8)2+(5−6)2 ⇒PA=(−4)2+(−1)2 ⇒PA=17 ⇒PA=4.123 \begin{aligned} & \Rightarrow PA=\sqrt{{{\left( 4-8 \right)}^{2}}+{{\left( 5-6 \right)}^{2}}} \\\ & \Rightarrow PA=\sqrt{{{(-4)}^{2}}+{{(-1)}^{2}}} \\\ & \Rightarrow PA=\sqrt{17} \\\ & \Rightarrow PA=4.123 \\\ \end{aligned}

Therefore the circumradius is 4.123 and the circumcenter is (4,5).

Note: Students may also be asked to calculate the orthocenter, centroid and many more. The general properties of these would make it useful to solve the problem easily. The circumcenter of the triangle may lie inside or even outside of the triangle.