Question

Find the coordinates of a point $A$, where $AB$, the diameter of a circle whose centre is $\left( {2, - 3} \right)$ and B is $\left( {1,4} \right)$.

Answer 1

Here, we have to find the coordinate of $A$, for that we use the formula for midpoint.
First we have to find Coordinate of the $x$ axis and $y$ axis.
Finally we get the required answer.

Complete step-by-step answer:

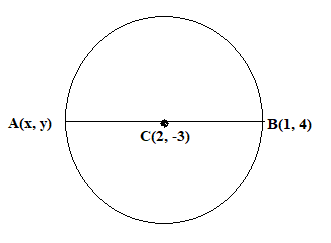
It is given that the circle with centre ${\text{C}}(2, - 3)$ and $AB$ is the diameter of circle with $B(1,4)$
We have to find the coordinates of a point $A$.
Let we consider $(x,y)$ to be the coordinate of $A$.
Since $AB$ is the diameter of the circle,
Here, centre $C$ is the midpoint of $AB$
$x -$Coordinate of centre = $\dfrac{{{x_1} + {x_2}}}{2}$
$y -$Coordinate of centre= $\dfrac{{{y_1} + {y_2}}}{2}$
${x_1} = x$, ${y_1} = y$, ${x_2} = 1$,${y_2} = 4$
$x -$ Coordinate of centre = $\dfrac{{x + 1}}{2}$
$y -$ Coordinate of centre = $\dfrac{{y + 4}}{2}$
But given that centre of circle is $(2, - 3)$ named as $(x,y)$
Therefore, we can write it as
$x - {\text{Coordinate}}$
$\dfrac{{x + 1}}{2} = 2$
after cross multiplication, we get
$x + 1 = 4$
Taking the term $1$ as RHS,
$x = 4 - 1$
On subtracting we get,
$x = 3$
Also we can write it as,
$y -$Coordinate
$\dfrac{{y + 4}}{2} = - 3$
after cross multiplication, we get
$y + 4 = - 6$
Taking the terms $4$ as RHS,
$y = - 6 - 4$
On subtracting we get,
$y = - 10$
Thus, the coordinate of $A$ is $(3, - 10)$
Hence the answer is $(3, - 10)$

Note: The above sum is the centre and a point is given, ask to find the other coordinate, mostly questions will be asked about what is the centre of the circle when the two points given, for that we use the above formula to derive the sum.
The coordinates we chosen for $A$ is $(x,y)$,
Suppose point $A$ is given and we have to find centre $C$, it is very easy use
$x -$ Coordinate of centre = $\dfrac{{{x_1} + {x_2}}}{2}$ to find $x -$ coordinate of centre.
Similarly, $y -$ coordinate of centre = $\dfrac{{{y_1} + {y_2}}}{2}$ to find $y -$ coordinate of centre.
Hence the centre is obtained.