Solveeit Logo
Login

Question

Question: Find the common tangents of the circles \[{x^2} + {y^2} = 1\] and\[{\left( {x - 1} \right)^2} + {\le...

Find the common tangents of the circles x2+y2=1{x^2} + {y^2} = 1 and(x−1)2+(y−3)2=4{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 4.

Explanation

Solution

Hint: First of all, find the centre and radius of the given circles and find the internal and external centre of similitudes. Then find the pair of transverse common tangents and direct common tangents to the given circles. S, use this concept to reach the solution.
Complete step-by-step answer:
Given circle equations are (x−1)2+(y−3)2=4{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 4 and x2+y2=1{x^2} + {y^2} = 1
We know that for the circle equation (x−h)2+(y−k)2=a2{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {a^2} the centre of the circle is (h,k)\left( {h,k} \right) and radius of the circle is aa.
So, for the circle equation (x−1)2+(y−3)2=4{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 4 the centre is C1(1,3){C_1}\left( {1,3} \right) and radius is r1=2{r_1} = 2.
We know that for the circle equation x2+y2=a2{x^2} + {y^2} = {a^2} the centre of the circle is (0,0)\left( {0,0} \right) and radius of the circle is aa.
So, for the circle equation x2+y2=1{x^2} + {y^2} = 1 the centre is C2(0,0){C_2}\left( {0,0} \right) and radius is r2=1{r_2} = 1.
We know that the distance between the points (x1,y1)\left( {{x_1},{y_1}} \right) and (x2,y2)\left( {{x_2},{y_2}} \right) is given by (x2−x1)2+(y2−y1)2\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} .
Now, consider the distance between the centres of the two circles i.e.,
C1C2=(1−0)2+(3−0)2=10{C_1}{C_2} = \sqrt {{{\left( {1 - 0} \right)}^2} + {{\left( {3 - 0} \right)}^2}} = \sqrt {10}
As C1C2>r1+r2⇒10>2+1{C_1}{C_2} > {r_1} + {r_2} \Rightarrow \sqrt {10} > 2 + 1, there will be four common tangents to the circles as shown in the below figure:

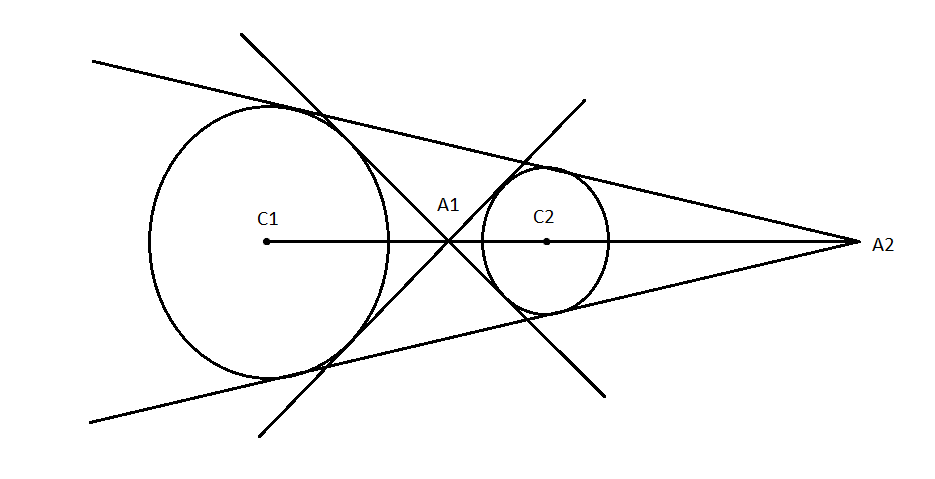
We know that if a point CC divides the two points A(x1,y1)A\left( {{x_1},{y_1}} \right) and B(x2,y2)B\left( {{x_2},{y_2}} \right) in the ratio p:qp:q the point CC is given by C=(px2+qx1p+q,py2+qy1p+q)C = \left( {\dfrac{{p{x_2} + q{x_1}}}{{p + q}},\dfrac{{p{y_2} + q{y_1}}}{{p + q}}} \right).
So, the internal centre of similitude, A1{A_1} divides C1C2{C_1}{C_2} in the ratio 2:12:1 internally is given by

⇒A1=(2(1)+1(0)2+1,2(3)+1(0)2+1) ∴A1=(23,63)=(23,2)  \Rightarrow {A_1} = \left( {\dfrac{{2\left( 1 \right) + 1\left( 0 \right)}}{{2 + 1}},\dfrac{{2\left( 3 \right) + 1\left( 0 \right)}}{{2 + 1}}} \right) \\\ \therefore {A_1} = \left( {\dfrac{2}{3},\dfrac{6}{3}} \right) = \left( {\dfrac{2}{3},2} \right) \\\

We know that the equation to the pair of transverse common tangents at point (h,k)\left( {h,k} \right) to the circle x2+y2=a2{x^2} + {y^2} = {a^2} is given by (xh+yk−a2)2=(h2+k2−a2)(x2+y2−a2){\left( {xh + yk - {a^2}} \right)^2} = \left( {{h^2} + {k^2} - {a^2}} \right)\left( {{x^2} + {y^2} - {a^2}} \right)
So, equation to the pair of transverse common tangents at (23,2)\left( {\dfrac{2}{3},2} \right) to the circle x2+y2=1{x^2} + {y^2} = 1 is

⇒(x(23)+y(2)−1)2=((23)2+(2)2−1)(x2+y2−1) ⇒(2x3+2y−1)2=(49+4−1)(x2+y2−1)  \Rightarrow {\left( {x\left( {\dfrac{2}{3}} \right) + y\left( 2 \right) - 1} \right)^2} = \left( {{{\left( {\dfrac{2}{3}} \right)}^2} + {{\left( 2 \right)}^2} - 1} \right)\left( {{x^2} + {y^2} - 1} \right) \\\ \Rightarrow {\left( {\dfrac{{2x}}{3} + 2y - 1} \right)^2} = \left( {\dfrac{4}{9} + 4 - 1} \right)\left( {{x^2} + {y^2} - 1} \right) \\\

Opening the terms inside the brackets by using the formula (a+b+c)2=a2+b2+c2+2ab+2bc+2ca{\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca, we have

⇒(2x3)2+(2y)+(1)+2(2x3)(2y)+2(2y)(−1)+2(2x3)(−1)=(49+3)(x2+y2−1) ⇒4x29+4y2+1+8xy3−4y−4x3=(4+279)(x2+y2−1) ⇒4x2+36y2+9+24xy−36y−12x9=(319)(x2+y2−1)  \Rightarrow {\left( {\dfrac{{2x}}{3}} \right)^2} + \left( {2y} \right) + \left( 1 \right) + 2\left( {\dfrac{{2x}}{3}} \right)\left( {2y} \right) + 2\left( {2y} \right)\left( { - 1} \right) + 2\left( {\dfrac{{2x}}{3}} \right)\left( { - 1} \right) = \left( {\dfrac{4}{9} + 3} \right)\left( {{x^2} + {y^2} - 1} \right) \\\ \Rightarrow \dfrac{{4{x^2}}}{9} + 4{y^2} + 1 + \dfrac{{8xy}}{3} - 4y - \dfrac{{4x}}{3} = \left( {\dfrac{{4 + 27}}{9}} \right)\left( {{x^2} + {y^2} - 1} \right) \\\ \Rightarrow \dfrac{{4{x^2} + 36{y^2} + 9 + 24xy - 36y - 12x}}{9} = \left( {\dfrac{{31}}{9}} \right)\left( {{x^2} + {y^2} - 1} \right) \\\

Cancelling and grouping the common terms, we have

⇒4x2+24xy+36y2−36y−12x+9=31x2+31y2−31 ⇒31x2−4x2−24xy+31y2−36y2+12x+36y−31−9=0 ∴27x2−24xy−5y2+12x+36y−40=0  \Rightarrow 4{x^2} + 24xy + 36{y^2} - 36y - 12x + 9 = 31{x^2} + 31{y^2} - 31 \\\ \Rightarrow 31{x^2} - 4{x^2} - 24xy + 31{y^2} - 36{y^2} + 12x + 36y - 31 - 9 = 0 \\\ \therefore 27{x^2} - 24xy - 5{y^2} + 12x + 36y - 40 = 0 \\\

We know that if a point CC divides the two points A(x1,y1)A\left( {{x_1},{y_1}} \right) and B(x2,y2)B\left( {{x_2},{y_2}} \right) in the ratio p:qp:q the point CC is given by C=(px2+qx1p+q,py2+qy1p+q)C = \left( {\dfrac{{p{x_2} + q{x_1}}}{{p + q}},\dfrac{{p{y_2} + q{y_1}}}{{p + q}}} \right).
So, the external centre of similitude, A2{A_2} divides C1C2{C_1}{C_2} in the ratio 2:12:1 externally is given by

⇒A2=(2(1)−1(0)2−1,2(3)−1(0)2−1) ∴A2=(2,6)  \Rightarrow {A_2} = \left( {\dfrac{{2\left( 1 \right) - 1\left( 0 \right)}}{{2 - 1}},\dfrac{{2\left( 3 \right) - 1\left( 0 \right)}}{{2 - 1}}} \right) \\\ \therefore {A_2} = \left( {2,6} \right) \\\

We know that the equation to the pair of direct common tangents at point (h,k)\left( {h,k} \right) to the circle x2+y2=a2{x^2} + {y^2} = {a^2} is given by (xh+yk−a2)2=(h2+k2−a2)(x2+y2−a2){\left( {xh + yk - {a^2}} \right)^2} = \left( {{h^2} + {k^2} - {a^2}} \right)\left( {{x^2} + {y^2} - {a^2}} \right)
So, equation to the pair of direct common tangents at (2,6)\left( {2,6} \right) to the circle x2+y2=1{x^2} + {y^2} = 1 is

⇒(x(2)+y(6)−1)2=((2)2+(6)2−1)(x2+y2−1) ⇒(2x+6y−1)2=(4+36−1)(x2+y2−1)  \Rightarrow {\left( {x\left( 2 \right) + y\left( 6 \right) - 1} \right)^2} = \left( {{{\left( 2 \right)}^2} + {{\left( 6 \right)}^2} - 1} \right)\left( {{x^2} + {y^2} - 1} \right) \\\ \Rightarrow {\left( {2x + 6y - 1} \right)^2} = \left( {4 + 36 - 1} \right)\left( {{x^2} + {y^2} - 1} \right) \\\

Opening the terms inside the brackets, we have

⇒4x2+36y2+1+2(2x)(6y)+2(2x)(−1)+2(6y)(−1)=(39)(x2+y2−1) ⇒4x2+36y2+1+24xy−4x−12y=39x2+39y2−39 ⇒39x2−4x2+39y2−36y2−24xy+4x+12y−39−1=0 ∴35x2−24xy+3y2+4x+12y−40=0  \Rightarrow 4{x^2} + 36{y^2} + 1 + 2\left( {2x} \right)\left( {6y} \right) + 2\left( {2x} \right)\left( { - 1} \right) + 2\left( {6y} \right)\left( { - 1} \right) = \left( {39} \right)\left( {{x^2} + {y^2} - 1} \right) \\\ \Rightarrow 4{x^2} + 36{y^2} + 1 + 24xy - 4x - 12y = 39{x^2} + 39{y^2} - 39 \\\ \Rightarrow 39{x^2} - 4{x^2} + 39{y^2} - 36{y^2} - 24xy + 4x + 12y - 39 - 1 = 0 \\\ \therefore 35{x^2} - 24xy + 3{y^2} + 4x + 12y - 40 = 0 \\\

Thus, the common tangents are 27x2−24xy−5y2+12x+36y−40=027{x^2} - 24xy - 5{y^2} + 12x + 36y - 40 = 0 and 35x2−24xy+3y2+4x+12y−40=035{x^2} - 24xy + 3{y^2} + 4x + 12y - 40 = 0.
Note: The equation to the pair of transverse common tangents at point (h,k)\left( {h,k} \right) to the circle x2+y2=a2{x^2} + {y^2} = {a^2} is given by (xh+yk−a2)2=(h2+k2−a2)(x2+y2−a2){\left( {xh + yk - {a^2}} \right)^2} = \left( {{h^2} + {k^2} - {a^2}} \right)\left( {{x^2} + {y^2} - {a^2}} \right). The equation to the pair of direct common tangents at point (h,k)\left( {h,k} \right) to the circle x2+y2=a2{x^2} + {y^2} = {a^2} is given by (xh+yk−a2)2=(h2+k2−a2)(x2+y2−a2){\left( {xh + yk - {a^2}} \right)^2} = \left( {{h^2} + {k^2} - {a^2}} \right)\left( {{x^2} + {y^2} - {a^2}} \right).