Question
Question: Find the coefficient of \({{x}^{4}}\) in the expansion of \({{(2-4x+3{{x}^{2}})}^{-2}}\)....
Find the coefficient of x4 in the expansion of
(2−4x+3x2)−2.
Solution
- Hint: Assume that the roots of the quadratic expression 3x2−4x+2=0 are a and b. Hence write (3x2−4x+2)21 as 91((x−a)(x−b)1)2. Decompose (x−a)(x−b)1 into partial fractions by multiplying and dividing numerator by b−a and writing b-a as (x-a)-(x-b). Use the identity (a−b)2=a2−2ab+b2 and binomial theorem for non-integral powers and hence find the coefficient of x4 in the expansion of the term.
Complete step-by-step solution -
Let the roots of the quadratic expression 3x2−4x+2=0 be a and b.
Hence, we have
3x2−4x+2=3(x−a)(x−b)
Hence, the given expression(E say) becomes
E=91((x−a)(x−b)1)2
Inside the square term multiplying numerator and denominator by a-b, we get
E=9(a−b)21((x−a)(x−b)a−b)2
Writing a-b as (x-b)-(x-a) in the numerator, we get
E=9(a−b)21((x−a)(x−b)x−b−(x−a))2
Using ca+b=ca+cb, we get
E=9(a−b)21(x−a1−x−b1)2
Using the identity (a−b)2=a2−2ab+b2, we get
E=9(a−b)21((x−a)21+(x−b)21+(x−a)(x−b)2)
From the above procedure, we know that (x−a)(x−b)1=a−b1(x−a1−x−b1)
Hence, we have
E=9(a−b)21((x−a)21+(x−b)21+a−b2(x−a1−x−b1))
Consider the term (x−a)21
We know from binomial theorem for real exponents
(1+x)n=1+nx+2!n(n−1)x2+⋯
Hence, we have
(x−a)−2=a−2(1−ax)−2=a21(1+a2x+2!3!(ax)2+3!4!(ax)3+4!5!(ax)4+O(x5))
Hence the coefficient of x4 in the expansion of (x−a)21 is a65
Similarly, the coefficient of x4 in the expansion of (x−b)21 is b65
Consider the term x−a1
We know from binomial theorem for real exponents
(1+x)n=1+nx+2!n(n−1)x2+⋯
Hence, we have
(x−a)−1=−a−1(1−ax)−1=−a1(1+ax+(ax)2+(ax)3+(ax)4+O(x5))
Hence the coefficient of x4 in the expansion of (x−a)1 is −a51
Similarly, the coefficient of x4 in the expansion of x−b1 is −b51
Hence, the coefficient of x4 in the expansion of E is 9(a−b)21(a65+b65−a−b2(−a51+b51))=9(a−b)21((ab)65(a6+b6)−(a−b)(ab)52(a5−b5))
Dividing a5−b5 by a-b
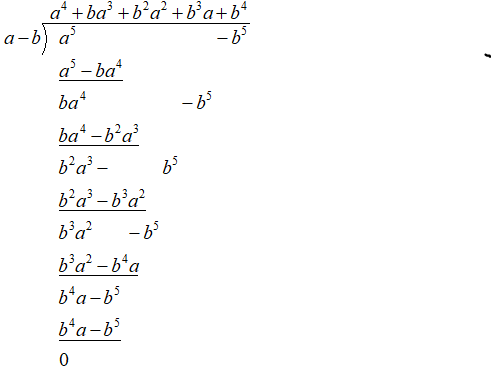
Hence, we have a−ba5−b5=(a4+b4+ab(a2+b2)+a2b2)
Hence, the coefficient of x4 in the expansion of E is
9(a−b)21((ab)65(a6+b6)−(ab)52(a4+b4+ab(a2+b2)+a2b2))
Now, we have a+b=34,ab=32
Hence, we have
(a−b)2=(a+b)2−4ab=916−38=9−8
Also, we have
a2+b2=(a+b)2−2ab=916−34=94a4+b4=(a2+b2)2−2(ab)2=8116−2×94=8116−98=81−56a6+b6=(a2+b2)(a4+b4−(ab)2)=94(81−56−94)=729−368
Hence, we have
The coefficient of x4 in the expansion of E is
9(9−8)1(32)65(729−368)+(32)52(81−56+32(94)+(32)2)=1659
Hence the coefficient of x4 in the expansion of (2−4x+3x2)−2 is 1659
Note: These types of questions usually involve long and cumbersome calculations, and hence a student is likely to make calculation mistakes. So we should try to minimise calculations as much as possible. In the above question, we minimise our calculation by converting to partial fractions and finding the coefficients of individual terms in summation rather than in product which made the calculations relatively easy.
