Solveeit Logo
Login

Question

Question: Find the circumcentre of the triangle formed by the points (2, 3), (1, – 5) and (– 1, 4). \[\left(...

Find the circumcentre of the triangle formed by the points (2, 3), (1, – 5) and (– 1, 4).
(a)(910,710)\left( a \right)\left( \dfrac{9}{10},\dfrac{7}{10} \right)
(b)(−910,710)\left( b \right)\left( \dfrac{-9}{10},\dfrac{7}{10} \right)
(c)(−910,710)\left( c \right)\left( \dfrac{-9}{10},\dfrac{7}{10} \right)
(d)(−910,−710)\left( d \right)\left( \dfrac{-9}{10},\dfrac{-7}{10} \right)

Explanation

Solution

The circumcentre is the point that is equidistant from all the vertices. We assume its co-ordinate as O(x, y) and then we will use the distance formula D=(x2−x1)2+(y2−y1)2D=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} to find AO, BO and CO. Once, we have AO, BO and CO, we will compare them to find the relation between x and y. Then we will use the elimination method to find x and y.

Complete step-by-step solution:
We are given a triangle with vertex A (2, 3), B (1, – 5), and C (– 1, 4). We have to find the circumcentre of triangle ABC. We know that the circumcentre is the point in triangle ABC which is equidistant from each vertex.
Let us assume the circumcentre is at O (x, y), then AO, BO, and CO all have the same distance.

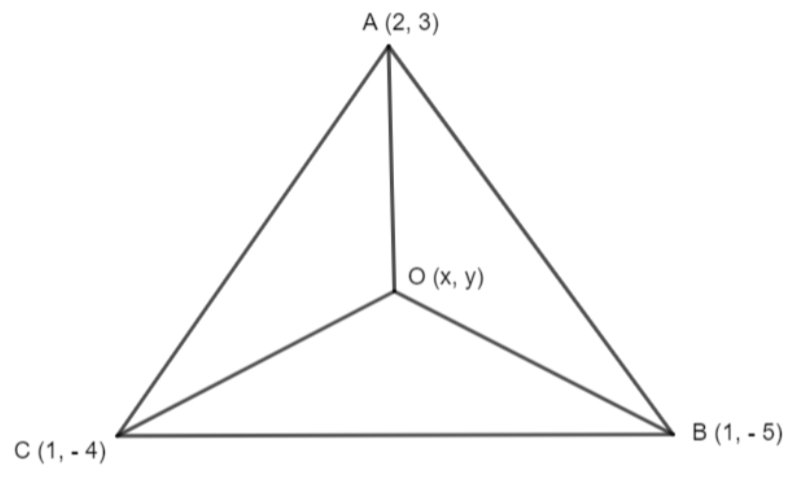
Now, we will find the distance AO, BO and CO. We know that the distance formula is given as
D=(x2−x1)2+(y2−y1)2D=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}
So, for A (2, 3) and O (x, y), AO is given as,
AO=(2−x)2+(3−y)2AO=\sqrt{{{\left( 2-x \right)}^{2}}+{{\left( 3-y \right)}^{2}}}
Now, for B (1, – 5) and O (x, y), BO is given as,
BO=(1−x)2+(−5−y)2BO=\sqrt{{{\left( 1-x \right)}^{2}}+{{\left( -5-y \right)}^{2}}}
And similarly, for C (– 1, 4) and O (x, y), CO is given as,
CO=(−1−x)2+(4−y)2CO=\sqrt{{{\left( -1-x \right)}^{2}}+{{\left( 4-y \right)}^{2}}}
Now, as AO = BO = CO, so we will first compare AO = BO. We will get,
BO=AOBO=AO
⇒(1−x)2+(−5−y)2=(2−x)2+(3−y)2\Rightarrow \sqrt{{{\left( 1-x \right)}^{2}}+{{\left( -5-y \right)}^{2}}}=\sqrt{{{\left( 2-x \right)}^{2}}+{{\left( 3-y \right)}^{2}}}
Squaring both the sides, we get,
⇒(1−x)2+(−5−y)2=(2−x)2+(3−y)2\Rightarrow {{\left( 1-x \right)}^{2}}+{{\left( -5-y \right)}^{2}}={{\left( 2-x \right)}^{2}}+{{\left( 3-y \right)}^{2}}
Opening the brackets, we get,
⇒1+x2−2x+25+y2+10y=4+x2−4x+9+y2−6y\Rightarrow 1+{{x}^{2}}-2x+25+{{y}^{2}}+10y=4+{{x}^{2}}-4x+9+{{y}^{2}}-6y
Simplifying, we get,
⇒2x+16y=−13.......(i)\Rightarrow 2x+16y=-13.......\left( i \right)
Now, comparing AO and CO, we get,
AO=COAO=CO
⇒(2−x)2+(3−y)2=(−1−x)2+(4−y)2\Rightarrow \sqrt{{{\left( 2-x \right)}^{2}}+{{\left( 3-y \right)}^{2}}}=\sqrt{{{\left( -1-x \right)}^{2}}+{{\left( 4-y \right)}^{2}}}
Squaring both the sides, we get,
⇒(2−x)2+(3−y)2=(−1−x)2+(4−y)2\Rightarrow {{\left( 2-x \right)}^{2}}+{{\left( 3-y \right)}^{2}}={{\left( -1-x \right)}^{2}}+{{\left( 4-y \right)}^{2}}
Opening the brackets, we get,
⇒4+x2−4x+9+y2−6y=1+x2+2x+16+y2−8y\Rightarrow 4+{{x}^{2}}-4x+9+{{y}^{2}}-6y=1+{{x}^{2}}+2x+16+{{y}^{2}}-8y
Simplifying further we get,
⇒−6x+2y=4......(ii)\Rightarrow -6x+2y=4......\left( ii \right)
Now, we will solve for equation (i) and (ii) to get the value of x and y. We will get,
eq(i)×3+eq(ii)eq\left( i \right)\times 3+eq\left( ii \right)

& 6x+48y=-39 \\\ & \underline{-6x+2y=4} \\\ & 50y=-35 \\\ \end{aligned}$$ Now, solving for y, we will get, $$\Rightarrow y=\dfrac{-35}{50}$$ Simplifying further we get, $$\Rightarrow y=\dfrac{-7}{10}$$ Now, we will put $$y=\dfrac{-7}{10}$$ in equation (ii), we get, $$\Rightarrow -6x+2y=4$$ $$\Rightarrow -6x+2\left( \dfrac{-7}{10} \right)=4$$ Now, solving for x, we get, $$\Rightarrow -6x+\dfrac{-7}{5}=4$$ $$\Rightarrow -6x=4+\dfrac{7}{5}$$ Simplifying, we get, $$\Rightarrow -6x=\dfrac{27}{5}$$ Dividing both the sides by – 6, we get, $$\Rightarrow x=\dfrac{-9}{10}$$ So, we get, $$x=\dfrac{-9}{10}$$ and $$\Rightarrow y=\dfrac{-7}{10}$$ Hence, the circumcentre coordinate is $$O\left( \dfrac{-9}{10},\dfrac{-7}{10} \right).$$ **Note:** Remember that $${{\left( -1-y \right)}^{2}}\ne {{1}^{2}}+{{y}^{2}}-2y.$$ It is $${{\left( -1-y \right)}^{2}}={{\left[ -\left( 1+y \right) \right]}^{2}}={{\left( -1 \right)}^{2}}{{\left( 1+y \right)}^{2}}={{\left( 1+y \right)}^{2}}.$$ So, we get, $${{\left( -1-y \right)}^{2}}={{\left( 1+y \right)}^{2}}={{1}^{2}}+{{y}^{2}}+2y.$$ In the elimination method, we make one of the coefficients equal and then add and subtract to get rid of them. Then we eliminate x, so we get only y and solve for y.