Question

Find the chord of contact of the tangents to the parabola ${{y}^{2}}=12x$ drawn through the point $\left( -1,2 \right)$.

Answer 1

Compare ${{y}^{2}}=12x$ with ${{y}^{2}}=4ax$ and find the value of a. Write the equation of tangent of parabola as $y=mx+\dfrac{a}{m}$, where $m$ is the slope of the tangent line. Substitute the given point $\left( -1,2 \right)$ in the equation of tangent and find the values of $m$. Substitute the values of $m$in the equation of the tangent to obtain the tangents of the given parabola. Finally, solve the equation of each tangent with the parabola to obtain the points of contact.

Complete step-by-step solution:
The figure shown below shows the situation graphically.

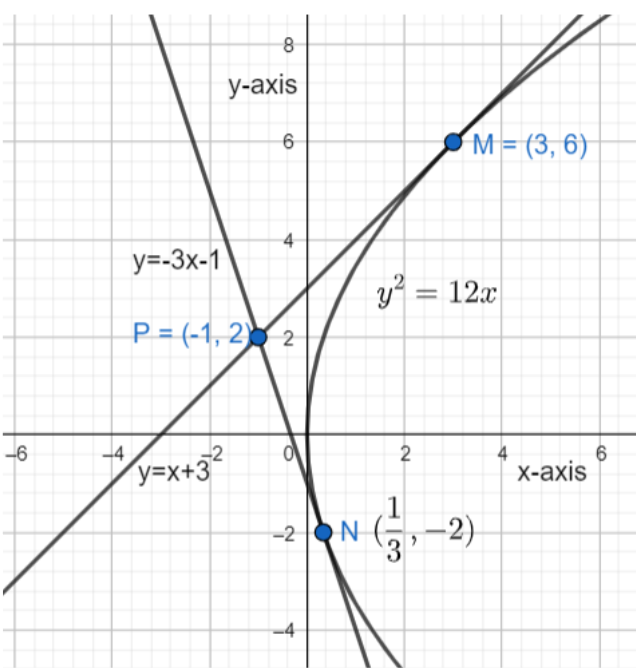
Here, we have to find the chord of contact of the tangents to the parabola ${{y}^{2}}=12x$ drawn through the point $\left( -1,2 \right)$. So, we have to determine the coordinates at which the tangents touch the parabola. Therefore, let us find the equation of tangents.
Comparing ${{y}^{2}}=12x$ with the general equation of parabola ${{y}^{2}}=4ax$, we get.
$\begin{aligned} & 4a=12 \\\ & \Rightarrow a=3 \\\ \end{aligned}$
Now, we know that the equation of a parabola is given as $y=mx+\dfrac{a}{m}$, where $m$ is the slope. Therefore, substituting the value of a in the equation of tangent, we get,
$\Rightarrow y=mx+\dfrac{3}{m}$
Since, it is given that the above equation is drawn through the point $\left( -1,2 \right)$. So, substituting this point in the above equation, we get,
$\begin{aligned} & \Rightarrow 2=-m+\dfrac{3}{m} \\\ & \Rightarrow 2m=-{{m}^{2}}+3 \\\ & \Rightarrow {{m}^{2}}+2m-3=0 \\\ \end{aligned}$
Applying the middle term split method, we get,
$\begin{aligned} & \Rightarrow {{m}^{2}}+3m-m-3=0 \\\ & \Rightarrow \left( m+3 \right)\left( m-1 \right)=0 \\\ & \Rightarrow m=1\text{ }or\text{ }-3 \\\ \end{aligned}$
So, substituting the values of $m$ in the equation of tangent, we get,
$\begin{aligned} & y=x+3\ldots \ldots \ldots \left( i \right) \\\ & y=-3x-1\ldots \ldots \ldots \left( ii \right) \\\ \end{aligned}$
Now, to find the chord of contact we have to solve the equations of tangent with the equation of parabola one by one. So, we have,
1. Consider $y=x+3$ and ${{y}^{2}}=12x$.
Substituting the value of $y$ from equation of tangent in the equation of parabola, we get,
$\begin{aligned} & \Rightarrow {{\left( x+3 \right)}^{2}}=12x \\\ & \Rightarrow {{x}^{2}}+9+6x=12x \\\ & \Rightarrow {{x}^{2}}+9-6x=0 \\\ & \Rightarrow {{\left( x-3 \right)}^{2}}=0 \\\ & \Rightarrow x=3 \\\ \end{aligned}$
Substituting $x=3$ in $y=x+3$, we get,
$\Rightarrow y=3+3=6$
Therefore, the point of contact is $\left( 3,6 \right)$.
2. Consider $y=-3x-1$ and ${{y}^{2}}=12x$.
Substituting the value of $y$ from equation of tangent in the equation of parabola, we get,
$\begin{aligned} & \Rightarrow {{\left( -3x-1 \right)}^{2}}=12x \\\ & \Rightarrow 9{{x}^{2}}+1+6x=12x \\\ & \Rightarrow 9{{x}^{2}}+1-6x=0 \\\ & \Rightarrow {{\left( 3x-1 \right)}^{2}}=0 \\\ & \Rightarrow x=\dfrac{1}{3} \\\ \end{aligned}$
Substituting $x=\dfrac{1}{3}$ in $y=-3x-1$ , we get,
$\Rightarrow y=-3\times \dfrac{1}{3}-1=-2$
Therefore, the point of contact is $\left( \dfrac{1}{3},-2 \right)$.
Hence, the point of chord of contact of the tangents to the parabola are $\left( 3,6 \right)$ and $\left( \dfrac{1}{3},-2 \right)$.

Note: One may note that if we have to find the equation of chord of contact then we will assume $M\left( 3,6 \right)$ and $N\left( \dfrac{1}{3},-2 \right)$ as $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in the above figure. Then we will apply the formula for general equation of line given as $\left( y-{{y}_{1}} \right)=\left( \dfrac{{{y}_{1}}-{{y}_{2}}}{{{x}_{1}}-{{x}_{2}}} \right)\left( x-{{x}_{1}} \right)$ and substitute the assumed values. To solve the above question, you must remember the general equation of tangent of parabola.