Question

Find the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are 100g, 150g and 200g respectively. Each side of the equilateral triangle is 0.5m long.

Answer 1

First we need to define the coordinates for the given masses. The centre of mass of the system of given masses can be calculated by taking the ratio of sum of products of the masses and their distances from the origin to the sum of the given masses.
Formula used:
The centre of mass of a system of mass can be given as
$C = \dfrac{{\sum {{m_i}r_i^2} }}{{\sum {{m_i}} }}$
Here ${m_i}$ represents the mass of the ith particle while ${r_i}$ represents the distance of the ith mass from the origin.

Detailed step by step solution:
The centre of mass of a system of masses is defined as the point on a body about which the whole mass of the given system is concentrated. Mathematically, it is equal to the ratio of sum of products of the masses and their distances from the origin to the sum of the given masses.
We are given three particles whose masses are given as
$\begin{array}{l} {m_1} = 100g\\\ {m_2} = 150g\\\ {m_3} = 200g \end{array}$
These three particles are arranged on the vertices of an equilateral triangle. Each side of the equilateral triangle has length of 0.5 m. We can draw the following diagram for this arrangement.

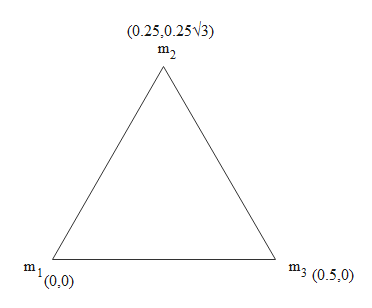
Now based on this diagram, we have three masses and their coordinates. Now we can find the coordinates of the centre of mass by using the formula given in equation (i). First, let us calculate the x-coordinate of the centre of mass. For this we will use the x-coordinates of the given masses. This is done in the following way.
$\begin{array}{l} \left( {{x_1},{y_1}} \right) = \left( {0,0} \right)\\\ \left( {{x_2},{y_2}} \right) = \left( {0.5,0} \right)\\\ \left( {{x_3},{y_3}} \right) = \left( {0.25,0.25\sqrt 3 } \right)\\\ {x_{CM}} = \dfrac{{{m_1}{x_1} + {m_2}{x_2} + {m_3}{x_3}}}{{{m_1} + {m_2}\, + {m_3}}}\\\ = \dfrac{{\left( {100 \times 0} \right) + \left( {150 \times 0.5} \right) + \left( {200 \times 0.25} \right)}}{{\left( {100 + 150 + 200} \right)}}\\\ \therefore {x_{CM}} = 0.278 \end{array}$
Similarly, we need to calculate the y-coordinate also which can be calculated in the following.
$\begin{array}{l} {y_{CM}} = \dfrac{{{m_1}{y_1} + {m_2}{y_2} + {m_3}{y_3}}}{{{m_1} + {m_2}\, + {m_3}}}\\\ = \dfrac{{\left( {100 \times 0} \right) + \left( {150 \times 0} \right) + \left( {200 \times 0.25\sqrt 3 } \right)}}{{\left( {100 + 150 + 200} \right)}}\\\ \therefore {y_{CM}} = 0.192 \end{array}$
Hence, the coordinates of the centre of mass are given as $\left( {0.278,0.192} \right)$.
Note: We have derived the coordinates of the various masses by using simple rules of Pythagoras theorem. We take the first mass at origin and derive the coordinates of the rest of the particles based on given information and properties of the equilateral triangle.