Question

Find the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particle are 100g, 150g, and 200g respectively. Each side of the equilateral triangle is 0.5 m long.

Answer 1

Recall the formula for the centre of mass. Express the centre of mass about the x-axis and about y-axis separately. The centre of mass about the x-axis and about y-axis are the coordinates of the centre of mass of the equilateral triangle.

Formula used:
${X_{CM}} = \dfrac{{{r_1}{m_1} + {r_2}{m_2} + {r_3}{m_3}}}{{{m_1} + {m_2} + {m_3}}}$
Here, r is the distance of each particle from the origin and m is the mass of each particle.

Complete Step by Step Answer:
Let the three particles are situated at the vertices of the triangle as shown in the figure below.

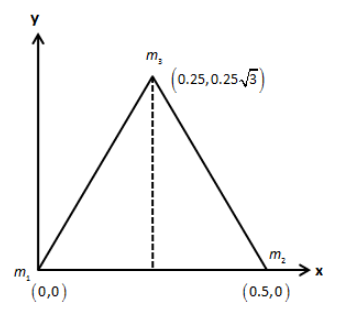
Since the triangle is in the xy-plane, it will have a centre of mass about the x-axis and about y-axis.Let us express the centre of mass of the above triangle about x-axis as follows,
${X_{CM}} = \dfrac{{{r_1}{m_1} + {r_2}{m_2} + {r_3}{m_3}}}{{{m_1} + {m_2} + {m_3}}}$
Here, r is the horizontal distance of each particle from the origin and m is the mass of each particle.

Since the particle ${m_1}$ is situated at the origin, the distance ${r_1}$ is zero.Substituting 0 for ${r_1}$, 0.5 m for ${r_2}$, 0.25 m for ${r_3}$, 100 g for ${m_1}$, 150g for ${m_2}$ and 200g for ${m_3}$ in the above equation, we get,
${X_{CM}} = \dfrac{{\left( 0 \right)\left( {100} \right) + \left( {0.5} \right)\left( {150} \right) + \left( {0.25} \right)\left( {200} \right)}}{{100 + 150 + 200}}$
$\Rightarrow {X_{CM}} = \dfrac{{125}}{{450}}$
$\Rightarrow {X_{CM}} = 0.28\,{\text{m}}$

Let us express the centre of mass of the above triangle about y-axis as follows,
${Y_{CM}} = \dfrac{{{r_1}{m_1} + {r_2}{m_2} + {r_3}{m_3}}}{{{m_1} + {m_2} + {m_3}}}$
Here, r is the vertical distance of each particle from the origin and m is the mass of each particle.
Since the particle ${m_1}$ and ${m_2}$ are situated on the x-axis, the distance ${r_1}$ and ${r_2}$ is zero.Substituting 0 for ${r_1}$, 0 for ${r_2}$, $0.25\sqrt 3$ m for ${r_3}$, 100 g for ${m_1}$, 150g for ${m_2}$ and 200g for ${m_3}$ in the above equation, we get,
${Y_{CM}} = \dfrac{{\left( 0 \right)\left( {100} \right) + \left( 0 \right)\left( {150} \right) + \left( {0.25\sqrt 3 } \right)\left( {200} \right)}}{{100 + 150 + 200}}$
$\Rightarrow {Y_{CM}} = \dfrac{{86.6}}{{450}}$
$\therefore {Y_{CM}} = 0.19\,{\text{m}}$

Thus, the centre of mass of the equilateral triangle is ${X_{CM}} = 0.28\,{\text{m}}$ and ${Y_{CM}} = 0.19\,{\text{m}}$.

Note: The rod, wire, etc, are one dimensional objects and therefore the centre of mass of these objects is measured from the one end of the rod. In the case of an equilateral triangle, the centre of mass is expressed as x and y-coordinates of the position of the centre of mass. The coordinates of the centre of mass of the above equilateral triangle are (0.28, 0.19).