Question

Find the centre of mass of a uniform
(i) half-disc,
(ii) quarter-disc.

Answer 1

The centre of mass of a mass distribution in space is the particular point in space where the weighted relative location of the distributed mass amounts to zero, according to physics. A force may be applied to this point to induce a linear acceleration without causing an angular acceleration.

Complete step-by-step answer:
In the case of a single rigid body, the centre of mass is set in relation to the body, and it would be located at the centroid if the body has uniform density. The centre of mass of hollow or open-shaped objects, such as a horseshoe, can also be found outside the human body. The centre of mass may not correspond to the location of any particular member of the system in the case of a distribution of different bodies, such as the planets of the Solar System.
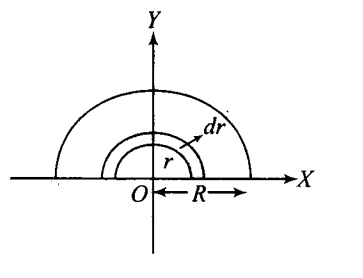self made
Let M be the mass of the half disc.
Area of the half disc = $\dfrac{{\pi {R^2}}}{2}$
Let mass per unit area be = ${\text{m}} = \dfrac{{2M}}{{\pi {R^2}}}$
(i) The half disc can be separated into a significant number of semicircular strips with mass dm, thickness dr, and radii ranging from 0 to R.

$dr = \dfrac{\pi }{2}\left[ {{{(r + dr)}^2} - {r^2}} \right]$

$dr = \dfrac{\pi }{2}\left[ {{r^2} + d{r^2} + 2rdr - {r^2}} \right]$

Suppose $d{r^2}$ is very small

$= \dfrac{\pi }{2}(2r \times dr)$

$= \pi rdr$

Hence mass of the strip be
$dm = \pi rdr \times \dfrac{{2{\text{M}}}}{{\pi {{\text{R}}^2}}}$
$dm = \dfrac{{2{\text{M}}}}{{{{\text{R}}^2}}} \cdot rdr$

Suppose (x,y) be the coordinates of Centre of mass
$So,(x,y) = \left( {0,\dfrac{{2r}}{\pi }} \right)$
Hence${\text{x}} = 0,{\text{y}} = \dfrac{{2r}}{\pi }$
Consider x cm and y cm be the co-ordinate of the centre of mass of semi-circular strip. Then

{{\text{x}} = {{\text{x}}_{{\text{cm}}}} = \dfrac{1}{{\text{M}}}\int_0^{\text{R}} {\text{x}} dm = \int_0^{\text{R}} 0 {\text{dm}} = 0} \\\ {{\text{y}} = {{\text{y}}_{{\text{cm}}}} = \dfrac{1}{{\text{M}}}\int_0^{\text{R}} {\dfrac{{2r}}{\pi }} \times \dfrac{{2{\text{M}}}}{{{{\text{R}}^2}}}rdr = \dfrac{1}{{\text{M}}} \cdot \dfrac{{4{\text{M}}}}{{\pi {{\text{R}}^2}}}\int_0^{\text{R}} {{r^2}} dr} \\\ {\quad = \dfrac{4}{{\pi {{\text{R}}^2}}}\left[ {\dfrac{{{r^3}}}{3}} \right]_0^{\text{R}} = \dfrac{4}{{3\pi {{\text{R}}^2}}} \cdot {{\text{R}}^3}} \\\ {\therefore \quad {{\text{y}}_{{\text{cm}}}} = \dfrac{{4{\text{R}}}}{{3\pi }}} \end{array}$$ ${\text{ So, centre of mass of uniform half disc }} = \left( {0,\dfrac{{4R}}{{3\pi }}} \right)$ (ii) Let the mass per unit quadrant be $\dfrac{{\dfrac{M}{{\pi {R^2}}}}}{4} = \dfrac{{4M}}{{\pi {R^2}}}$ Similarly, for an half disc, along the x axis the centre of mass be ${\text{X}} = \dfrac{{4R}}{{3\pi }}$ So the centre of mass of quarter disc becomes $\left( {\dfrac{{4R}}{{3\pi }},\dfrac{{4R}}{{3\pi }}} \right)$ **Note:** The centre of mass is a valuable reference point for physics equations involving masses dispersed in space, such as celestial bodies' linear and angular momentum and rigid body dynamics. The equations of motion of planets was constructed as point masses found at the centres of mass in orbital mechanics. The centre of mass frame is an inertial frame in which a system's centre of mass is at rest in relation to the coordinate system's origin.