Question

Find the centre of mass of a uniform hollow hemisphere of radius R.

Answer 1

Consider a small ring element of the hemisphere, which makes an angle $\theta$ with the positive x-axis. Use the formula for the centre of mass of a system of particles. Assume that the hemisphere has uniform mass distribution and find the mass of the small element.
Formula used:
${{y}_{com}}=\dfrac{\int{dmy}}{M}$
$\sigma =\dfrac{M}{2\pi {{R}^{2}}}$

Complete answer:
Consider a hollow hemisphere of radius R as shown.
Due to symmetry, the x coordinate of the centre of mass of this surface will be zero.
Let us find the y component of the centre of mass.
For this, consider a small element of the hemisphere in a ring, as shown in the figure.

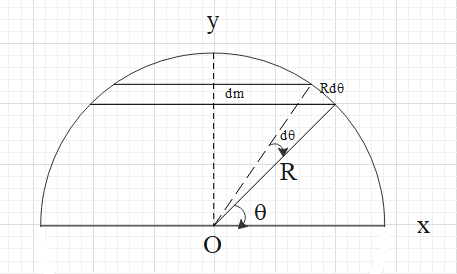
Let this ring make an angle $\theta$ with the positive x-axis and the width of this ring element subtend a small angle $d\theta$ at the origin.
The radius of this will be $R\cos \theta$ and the width will be equal to $Rd\theta$ (from the arc-length formula).
Now, centre of mass of a system of small elements is given as ${{y}_{com}}=\dfrac{\int{dmy}}{M}$ …(i)
Here, y is the position of the ring element on the y-axis, dm is the mass of this element and M is the total mass of the hemisphere.
To find dm, let us assume that the mass of the hemisphere is uniformly distributed. Therefore, it will have a uniform surface mass density.
The surface mass density of the hemisphere will be $\sigma =\dfrac{M}{2\pi {{R}^{2}}}$.
The surface mass density of the ring element will be $\sigma =\dfrac{dm}{2\pi R\cos \theta (Rd\theta )}$
$\Rightarrow \sigma =\dfrac{dm}{2\pi R\cos \theta (Rd\theta )}=\dfrac{M}{2\pi {{R}^{2}}}$
$\Rightarrow \dfrac{dm}{\cos \theta d\theta }=M$
$\Rightarrow dm=M\cos \theta d\theta$
From the figure we get that $y=R\sin \theta$
Substitute the values of dm and y in (i).
${{y}_{com}}=\dfrac{\int{M\cos \theta d\theta (R\sin \theta )}}{M}$
$\Rightarrow {{y}_{com}}=R\int{\cos \theta \sin \theta d\theta }$.
The limits of $\theta$ will be from 0 to $\dfrac{\pi }{2}$.
$\Rightarrow {{y}_{com}}=R\int\limits_{0}^{\pi /2}{\cos \theta \sin \theta d\theta }$ …. (ii)
We know that $\sin 2\theta =2\cos \theta \sin \theta$.
$\Rightarrow \cos \theta \sin \theta =\dfrac{\sin 2\theta }{2}$
Substitute this value in (ii).
$\Rightarrow {{y}_{com}}=R\int\limits_{0}^{\pi /2}{\dfrac{\sin 2\theta }{2}d\theta }$
$\Rightarrow {{y}_{com}}=\dfrac{R}{2}\int\limits_{0}^{\pi /2}{\sin 2\theta d\theta }$
$\Rightarrow {{y}_{com}}=-\dfrac{R}{2}\cos 2\theta |_{0}^{\pi /2}=-\dfrac{R}{2}\left( \cos \dfrac{\pi }{2}-\cos (0) \right)$
$\Rightarrow {{y}_{com}}=-\dfrac{R}{2}\left( 0-1 \right)=\dfrac{R}{2}$.
Therefore, the centre of mass of the hollow hemisphere is $\left( 0,\dfrac{R}{2} \right)$.

Note:
Students can make a mistake in writing the limits of the angle $\theta$. Some students may consider the limits of $\theta$ from 0 to $\pi$.
Note that we are considering small ring elements of the hemisphere. So the rings will start from the bottom of the hemisphere when the angle is zero. And the angle increases, we get the other rings. Therefore, at the ring element (at the top) the angle will be equal to $\dfrac{\pi }{2}$.