Question

Find the centre of mass of a non-uniform rod of length $L$, whose mass per unit length varies as $\rho =\dfrac{k\cdot {{x}^{2}}}{L}$ (where $k$ is a constant and $x$ is the distance of any point from one end) from the same end.
$\text{A}\text{. }\dfrac{3}{4}L$
$\text{B}\text{. }\dfrac{1}{4}L$
$\text{C}\text{. }\dfrac{1}{6}L$
$\text{D}\text{. }\dfrac{2}{3}L$

Answer 1

Hint: When the centre of mass of a body cannot be found using the axis of symmetry, it can be found by integration. Thickness or length of body can be divided into tiny strips, each with thickness $dx$. Integrate mass of each element multiplied by its respective position with respect to $x$ and divide by the integration of mass of each element. We will get the required position of centre of mass.

Formula used:
${{X}_{CM}}=\dfrac{\int\limits_{0}^{L}{xdm}}{\int\limits_{0}^{L}{dm}}$

Complete step by step answer:
The centre of mass of a distribution of mass in space is the unique point, an imaginary point in the body of matter, where the weighted relative position of all the distributed masses sums up to be zero. This is the point through which a force may be applied to cause some linear acceleration without an angular acceleration. For simple rigid bodies with uniform density, the centre of mass is located at the centroid. The centre of mass of any system is a point which represents the mean position of the matter in a body or system.
The centre of mass of a system can be calculated by taking the value of all the masses we are trying to find the centre of mass between and multiplying them by their positions. Then, we add these two and divide them by the sum of all the individual masses.
${{X}_{CM}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}+.....{{m}_{n}}{{x}_{n}}}{{{m}_{1}}+{{m}_{1}}+.....{{m}_{n}}}$
In case of a non-uniform rod, the position of centre of mass depends upon the density distribution of the rod.

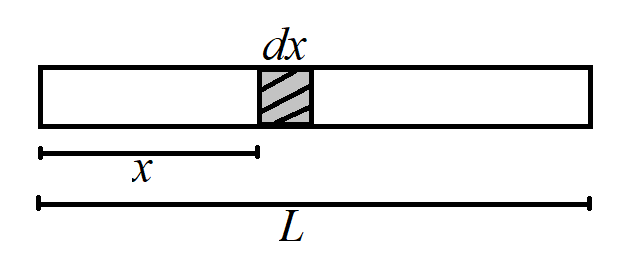
The centre of mass of a non-uniform rod is given by,
${{X}_{CM}}=\dfrac{\int\limits_{0}^{L}{xdm}}{\int\limits_{0}^{L}{dm}}$
Where,
$L$ is the length of the rod
$x$ is the position of mass element from one end of rod
${{X}_{CM}}=\dfrac{\int\limits_{0}^{L}{x\rho dx}}{\int\limits_{0}^{L}{\rho dx}}$
Where, $\rho =\dfrac{dm}{dx}$
We are given,
$\dfrac{dm}{dx}=\dfrac{k{{x}^{2}}}{L}$
Therefore, $dm=\dfrac{k{{x}^{2}}}{L}dx$
${{X}_{CM}}=\dfrac{\int\limits_{0}^{L}{x\dfrac{k{{x}^{2}}}{L}dx}}{\int\limits_{0}^{L}{\dfrac{k{{x}^{2}}}{L}dx}}$
${{X}_{CM}}=\dfrac{\dfrac{K}{L}\left[ \dfrac{{{x}^{4}}}{4} \right]_{0}^{L}}{\dfrac{K}{L}\left[ \dfrac{{{x}^{3}}}{3} \right]_{0}^{L}}=\dfrac{\dfrac{{{L}^{4}}}{4}-0}{\dfrac{{{L}^{3}}}{3}-0}$
${{X}_{CM}}=\dfrac{3L}{4}$
The centre of mass of a given rod is situated at a distance of $\dfrac{3L}{4}$from one end of the rod.
Hence, the correct option is A.

Note: If the rod has constant density $\rho$, given in terms of mass per unit length, then the mass of rod is just the product of the density and length of rod. In the above case we were given the density of rod in the form of mass per unit length, therefore, while integrating unit mass of rod, we took mass as the product of density of rod and the position of the unit mass from one end of the rod.