Question

Find the center of the circle passing through the points $\left( {6, - 6} \right),\left( {3, - 7} \right)$and $\left( {3,3} \right)$.

Answer 1

Hint: Name all the coordinates A,B and C. Draw a circle and name its center O. assume the coordinates of the center of the circle O to be $\left( {x,y} \right)$. After doing so, apply the formula by naming the coordinates of the points A,B and C as $\left( {{x_1},{y_1}} \right);\left( {{x_2},{y_2}} \right);\left( {{x_3},{y_3}} \right)$respectively, $\sqrt {{{\left( {x - {x_1}} \right)}^2} + {{\left( {y - {y_1}} \right)}^2}}$.

Complete step-by-step answer:

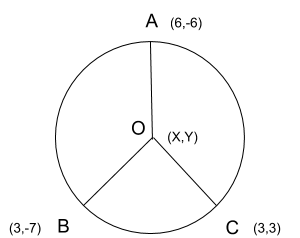
The coordinates given to us by the question are-
$\left( {6, - 6} \right),\left( {3, - 7} \right)$and $\left( {3,3} \right)$
Name the coordinates A, B and C respectively, we get-
$A = \left( {6, - 6} \right) \\\ B = \left( {3, - 7} \right) \\\$
And
$C = \left( {3,3} \right)$
Now, let the center of the circle be O and its coordinates be $\left( {x,y} \right)$
Since O is the center of the circle and the points A, B and C are on its circumference, then by property:
$OA = OB = OC = R$, where R is the radius of the circle.
now,
$A = \left( {6, - 6} \right) \Rightarrow {x_1} = 6,{y_1} = - 6 \\\ B = \left( {3, - 7} \right) \Rightarrow {x_2} = 3,{y_2} = - 7 \\\ C = \left( {3,3} \right) \Rightarrow {x_3} = 3,{y_3} = 3 \\\$
Since,
$OA = OB = OC$, then
$OA = OB \\\ OA = OC \\\$
Putting the formula $\sqrt {{{\left( {x - {x_1}} \right)}^2} + {{\left( {y - {y_1}} \right)}^2}}$ into OA, OB, and OC we get:
$OA = \sqrt {\left( {x - {x_1}} \right) + {{\left( {y - {y_1}} \right)}^2}} = \sqrt {{{\left( {x - 6} \right)}^2} + {{\left( {y + 6} \right)}^2}} \\\ \\\ OB = \sqrt {{{\left( {x - {x_2}} \right)}^2} + {{\left( {y - {y_2}} \right)}^2}} = \sqrt {{{\left( {x - 3} \right)}^2} + {{\left( {y - 3} \right)}^2}} \\\ \\\ OC = \sqrt {{{\left( {x - {x_3}} \right)}^2} + {{\left( {y - {y_3}} \right)}^2}} = \sqrt {{{\left( {x - 3} \right)}^2} + {{\left( {y + 7} \right)}^2}} \\\$

Name each equation mentioned above as equation 1, equation 2, and equation 3 respectively,

$OA = \sqrt {\left( {x - {x_1}} \right) + {{\left( {y - {y_1}} \right)}^2}} = \sqrt {{{\left( {x - 6} \right)}^2} + {{\left( {y + 6} \right)}^2}}$ $\to$ equation 1
$OB = \sqrt {{{\left( {x - {x_2}} \right)}^2} + {{\left( {y - {y_2}} \right)}^2}} = \sqrt {{{\left( {x - 3} \right)}^2} + {{\left( {y - 3} \right)}^2}}$ $\to$ equation 2
$OC = \sqrt {{{\left( {x - {x_3}} \right)}^2} + {{\left( {y - {y_3}} \right)}^2}} = \sqrt {{{\left( {x - 3} \right)}^2} + {{\left( {y + 7} \right)}^2}}$ $\to$ equation 3

Now, since we already discussed that $OA = OB = OC = R$ , we will put each equations equal to one another.
By putting $OA = OB$, which means by putting equation 1 and equation 2 equal to each other we get,
$\sqrt {{{\left( {x - 6} \right)}^2} + {{\left( {y + 6} \right)}^2}} = \sqrt {{{\left( {x - 3} \right)}^2} + {{\left( {y - 3} \right)}^2}}$
Squaring both sides, we get-
${x^2} + 36 - 12x + {y^2} + 36 + 12y = {x^2} + 9 - 6x + {y^2} - 6y + 9$
Cancelling ${x^2}$ and ${y^2}$ from both the sides,
$\- 6x + 18y = - 54 \\\ \Rightarrow x - 3y = 9 \\\$
Thus, mark the above equation as equation 4
$x - 3y = 9$ $\to$ equation 4
Similarly, putting $OA = OC$and squaring both sides we get,
${x^2} + 36 - 12x + {y^2} + 12y + 36 = {x^2} + 9 - 6x + {y^2} + 49 + 14y$
$\Rightarrow - 6x - 2y = - 14 \\\ \Rightarrow 3x + y = 7 \\\$
Naming the above equation as equation 5
$3x + y = 7$ $\to$ equation 5
Now, solve equation 4 and equation 5
Multiply both the sides of equation four by 3 then subtract equation five from equation four and we will get the value of x and y as:
$x = 3,y = - 2$
Hence, the coordinates of the center of the circle are $x = 3,y = - 2$.

Note: While subtracting, multiplying either one of the equations (sometimes both) by a number is necessary in order to make the equation balanced and to get the answer easily. These type of questions are always solved by using the formula $\sqrt {{{\left( {x - {x_1}} \right)}^2} + {{\left( {y - {y_1}} \right)}^2}}$ directly or indirectly.