Question

Find the center of mass of a uniform solid cone.

Answer 1

The center of a solid body can be calculated by taking a suitable cross section in the body, applying it in center of mass formula for continuous bodies and integrating it throughout to get the center of mass. Find out the value of centre of mass in terms of total height of the cone.

Complete answer:
We have the equation of centre of mass is,
$CM = \dfrac{{\int {\rho hdV} }}{{\int {\rho dV} }}$
Here, $\rho$ is the density of the body, h is the position of the centre of mass from the origin and V is the volume of the body.

Let’s consider the cone as shown in the following figure.

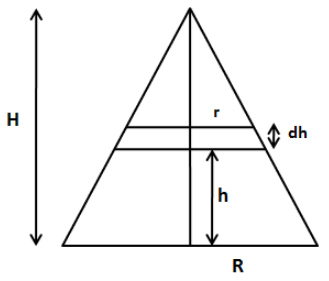
Let us consider the small disc of the cone of radius r and thickness dh situated at height h from the base of the cone as shown in the above figure.

From the geometry of the above figure, we can write,
$\dfrac{r}{R} = \dfrac{{H - h}}{H}$
$\Rightarrow r = \left( {\dfrac{{H - h}}{H}} \right)R$ …… (1)
Let’s express the volume of the small disc as follows,
$dV = \pi {r^2}dh$
Using equation (1), we can write,
$dV = \pi {\left( {\left( {\dfrac{{H - h}}{H}} \right)R} \right)^2}dh$ …… (2)

The centre of mass of the cone is,
$CM = \dfrac{{\int {\rho hdV} }}{{\int {\rho dV} }}$
Using equation (2) in the above equation, we get,
$CM = \dfrac{{\int {\rho h\pi {{\left( {\dfrac{{H - h}}{H}} \right)}^2}{R^2}dh} }}{{\int {\rho \pi {{\left( {\dfrac{{H - h}}{H}} \right)}^2}{R^2}dh} }}$
$\Rightarrow CM = \dfrac{{\dfrac{1}{{{H^2}}}\int {h{{\left( {H - h} \right)}^2}dh} }}{{\dfrac{1}{{{H^2}}}\int {{{\left( {H - h} \right)}^2}dh} }}$
$\Rightarrow CM = \dfrac{{\int {h{{\left( {H - h} \right)}^2}dh} }}{{\int {{{\left( {H - h} \right)}^2}dh} }}$

Substituting the limits of integration from 0 to H, we get,
${\text{CM}} = \dfrac{{\int\limits_0^H {h{{\left( {H - h} \right)}^2}dh} }}{{\int\limits_0^H {{{\left( {H - h} \right)}^2}dh} }}$
$\Rightarrow {\text{CM}} = \dfrac{{\int\limits_0^H {h\left( {{H^2} - 2Hh + {h^2}} \right)dh} }}{{\int\limits_0^H {\left( {{H^2} - 2Hh + {h^2}} \right)dh} }}$
$\Rightarrow {\text{CM}} = \dfrac{{{H^2}\int\limits_0^H h \,dh - 2H\int\limits_0^H {{h^2}} dh + \int\limits_0^H {{h^3}dh} }}{{{H^2}\int\limits_0^H {dh} - 2H\int\limits_0^H {h\,} dh + \int\limits_0^H {{h^2}dh} }}$
$\Rightarrow {\text{CM}} = \dfrac{{{H^2}\dfrac{{{H^2}}}{2} - 2H\dfrac{{{H^3}}}{3} + \dfrac{{{H^4}}}{4}}}{{{H^2}H - 2H\dfrac{{{H^2}}}{2} + \dfrac{{{H^3}}}{3}}}$
$\Rightarrow {\text{CM}} = \dfrac{{{H^4}\left( {\dfrac{1}{{12}}} \right)}}{{{H^3}\left( {\dfrac{1}{3}} \right)}}$
$\therefore {\text{CM}} = \dfrac{H}{4}$

Thus, the distance of centre of mass from the base of the cone is $\dfrac{H}{4}$.

Note: The center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weight relative position of the distributed mass sums to zero. This is the point at which a pass may be applied to cause a linear acceleration without an angular acceleration. The center of mass of the cone will always lie on its axis due to symmetry.