Question

Find the center of mass of a uniform semi-circular ring of radius $R$ and mass $m$.

Answer 1

The center of mass of an object is the point at which the total mass is supposed to be concentrated. For a semicircular ring, consider a mass per unit length. Then consider small differential length along the circumference of the semi-circular ring. Calculate the mass of this length. Center of mass is given as the sum of product of the mass from the point of origin. Integrate this product over the semi-circular ring and then divide the result by total mass.

Complete step by step solution:
Let us consider the center of the ring to be at the origin. Consider the following figure:

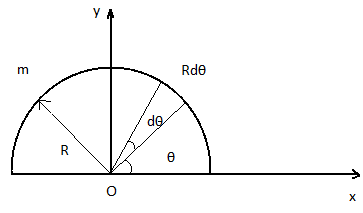
Here, we have a semicircular ring of mass $m$ and radius $R$.
Let the mass per unit length be $\lambda$ , having value as $\lambda = \dfrac{m}{{\pi R}}$ .
We have considered a differential element $dl$ such that $dl = Rd\theta$ .
Now the mass of this element will be $dm = \lambda Rd\theta$.
The centre of mass will be calculated along X-axis as well as Y-axis.
For this we need to consider the distance of the mass $dm$ . Along the X-axis the distance will be $Rsin\theta$ and the distance of this mass $dm$ along Y-axis will be $Rcos\theta$ .
Thus, the x-coordinate of the center of mass ${x_{cm}}$ will be:
${x_{cm}} = \dfrac{1}{m}\int {\left( {R\cos \theta } \right)} \lambda Rd\theta$
$\Rightarrow {x_{cm}} = \dfrac{1}{m}\int\limits_0^\pi {\left( {R\cos \theta } \right)} \lambda Rd\theta$
As $\theta$ lies between $\left[ {0,\pi } \right]$
$\Rightarrow {x_{cm}} = \dfrac{{\lambda {R^2}}}{m}\int\limits_0^\pi {\cos \theta d\theta }$
$\Rightarrow {x_{cm}} = \dfrac{{\lambda {R^2}}}{m}\left[ {\sin \theta } \right]_0^\pi$
$\Rightarrow {x_{cm}} = \dfrac{{\lambda {R^2}}}{m}\left[ {\sin \pi - \sin 0} \right]$
$\therefore {x_{cm}} = \dfrac{{\lambda {R^2}}}{m}\left[ 0 \right] = 0$
That is the x-coordinate of the centre of mass is zero which is true as the semi-circular ring has its centre at origin and it is equally divided along the Y-axis.
The y-coordinate of the centre of mass is:
${y_{cm}} = \dfrac{1}{m}\int {\left( {Rsin\theta } \right)} \lambda Rd\theta$
$\Rightarrow {y_{cm}} = \dfrac{{\lambda {R^2}}}{m}\int\limits_0^\pi {\left( {sin\theta } \right)} d\theta$
As $\theta$ lies between $\left[ {0,\pi } \right]$
$\Rightarrow {y_{cm}} = \dfrac{{\lambda {R^2}}}{m}\left[ { - \cos \theta } \right]_0^\pi$
$\Rightarrow {x_{cm}} = \dfrac{{\lambda {R^2}}}{m}\left[ { - 1\left( {\cos \pi - \cos 0} \right)} \right]$
$\Rightarrow {y_{cm}} = \dfrac{{\lambda {R^2}}}{m}\left[ { - 1\left( { - 1 - 1} \right)} \right]$
$\Rightarrow {y_{cm}} = \dfrac{{\lambda {R^2}}}{m} \times 2$
But $\lambda$ was mass per unit length, substituting $\lambda = \dfrac{m}{{\pi R}}$ , we get
$\Rightarrow {y_{cm}} = \dfrac{m}{{\pi R}} \times \dfrac{{{R^2}}}{m} \times 2$
$\therefore {y_{cm}} = \dfrac{{2R}}{\pi }$
Thus, the centre of mass of semi-circular ring lies at $\left( {0,\dfrac{{2R}}{\pi }} \right).$

Note: The quantity mass per unit length will remain constant as the ring is uniform thus, its mass is uniformly distributed along the circumference. The center of mass lies outside the ring and not on the surface of the ring. The distances for differential length are taken as components along X-axis and Y-axis.