Question
Question: Find the center of mass of a uniform \(L\) shaped lamina ( a thin flat plate) with dimensions as sho...
Find the center of mass of a uniform L shaped lamina ( a thin flat plate) with dimensions as shown. The mass of the lamina is 3Kg.
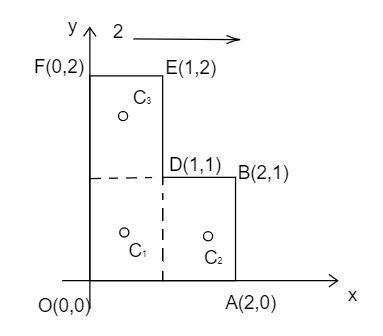
Solution
Divide the given diagram of the plane laminar into three squares as it helps in easy calculation. Find the coordinate point of the center of mass of the squares and substitute then in the formula of the center of mass given below to find the coordinate of the center of mass of the plane laminar.
Formula used:
The formula for the center of mass is given by
X=0∑nmn0∑nmnxn
Where X is the x- coordinate of the center of mass for the plane lamina, m is the mass of the square , x is the centre of mass of the square and n is the number of squares.
Complete step by step solution:
From the diagram, let us consider that there are three squares in the plane laminar. Hence the centre of masses of these squares helps to find out the common centre of mass of the lamina.
It is given that the mass of the plane lamina is 3Kg . Since all the three squares are equal, they must also have equal masses. Hence the mass of each square is 1Kg .
From the diagram, the centre of mass of the plane lamina is calculated. The centre of mass of the first square is (21,21), the centre of mass of the second square is (23,21) and the centre of mass of the third square is (21,23).
Using the formula of the centre of mass,
X=0∑nmn0∑nmnxn
Substituting the known values in the above formula,
⇒ X=1+1+121+23+21
By simplifying the above step,
⇒ X=65
Similarly calculating it for Y coordinate
Y=0∑nmn0∑nmnyn
⇒ Y=1+1+121+21+23
The value of the Y coordinate is obtained as 65 .
Hence the centre of mass of the plane lamina is located at (65,65).
Note: The centre of mass acts at the centre of the square. The value of the x and the y coordinate of the centre of masses of the square is found by measuring the distance between the x and the y coordinate axis and the centre of masses of the square.
