Question

Find the Cartesian equation of the line which passes through the point $\left( -2,4,-5 \right)$ and is parallel to the line $\dfrac{x+3}{3}=\dfrac{4-y}{5}=\dfrac{z+8}{6}$.

Answer 1

To solve this problem, we should know the relation the directional ratios of two parallel lines. The corresponding directional ratios of two parallel lines are proportional. Mathematically, if two lines with directional ratios $a,b,c$ and${{a}_{1}},{{b}_{1}},{{c}_{1}}$ respectively are parallel, the condition is $\dfrac{a}{{{a}_{1}}}=\dfrac{b}{{{b}_{1}}}=\dfrac{c}{{{c}_{1}}}$. The directional ratios of a line of the form $\dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=\dfrac{z-{{z}_{1}}}{c}$ are a, b, c respectively. Using this relation, we can get the directional ratios of the line $\dfrac{x+3}{3}=\dfrac{4-y}{5}=\dfrac{z+8}{6}$. From the relation of parallel lines, as given in the question, we can get the directional ratios of the required line. If the directional ratios of a line are a, b, c and the line pass through the point $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$, then the Cartesian equation of the line is given by the formula $\dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=\dfrac{z-{{z}_{1}}}{c}$. Using this equation with the obtained directional ratios from the parallel line and the condition that the line passes through the point A$\left( -2,4,-5 \right)$, we get the required equation of the line.

Complete step by step answer:
We can infer from the question that the required line is parallel to the line $\dfrac{x+3}{3}=\dfrac{4-y}{5}=\dfrac{z+8}{6}$.
We know that the condition for two lines to be parallel is that the corresponding directional ratios of the two lines should be proportional which is mathematically written as two lines with directional ratios $a,b,c$ and${{a}_{1}},{{b}_{1}},{{c}_{1}}$ respectively are parallel, the condition is $\dfrac{a}{{{a}_{1}}}=\dfrac{b}{{{b}_{1}}}=\dfrac{c}{{{c}_{1}}}$.
The directional ratios of a line of the form $\dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=\dfrac{z-{{z}_{1}}}{c}$ are a, b, c respectively.
Let us consider the given line $\dfrac{x+3}{3}=\dfrac{4-y}{5}=\dfrac{z+8}{6}$.
We can rewrite the equation as
$\dfrac{x+3}{3}=\dfrac{y-4}{-5}=\dfrac{z+8}{6}$
Comparing this equation with the above relation, we get the directional ratios of the line as
$\begin{aligned} & a=3 \\\ & b=-5 \\\ & c=6 \\\ \end{aligned}$
Let us consider the directional ratios of the required line be a, b, c respectively. We can write the relation between them from the condition of parallel lines as
$\begin{aligned} & \dfrac{a}{3}=\dfrac{b}{-5}=\dfrac{c}{6}=k \\\ & a=3k \\\ & b=-5k \\\ & c=6k \\\ \end{aligned}$
We know that, if the directional ratios of a line are a, b, c and the line pass through the point $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$, then the Cartesian equation of the line is given by the formula $\dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=\dfrac{z-{{z}_{1}}}{c}$.
We can infer that the required line passes through the point A$\left( -2,4,-5 \right)$.
From the above relation with
$\begin{aligned} & {{x}_{1}}=-2\text{ , }a=3k \\\ & {{y}_{1}}=4\text{ , }b=-5k \\\ & {{z}_{1}}=-5\text{ , }c=6k \\\ \end{aligned}$
We get the equation of the line as
$\dfrac{x-\left( -2 \right)}{3k}=\dfrac{y-4}{-5k}=\dfrac{z-\left( -5 \right)}{6k}$
Cancelling k in all the three terms, we get
$\begin{aligned} & \dfrac{x+2}{3}=\dfrac{y-4}{-5}=\dfrac{z+5}{6} \\\ & \dfrac{x+2}{3}=\dfrac{4-y}{5}=\dfrac{z+5}{6} \\\ \end{aligned}$

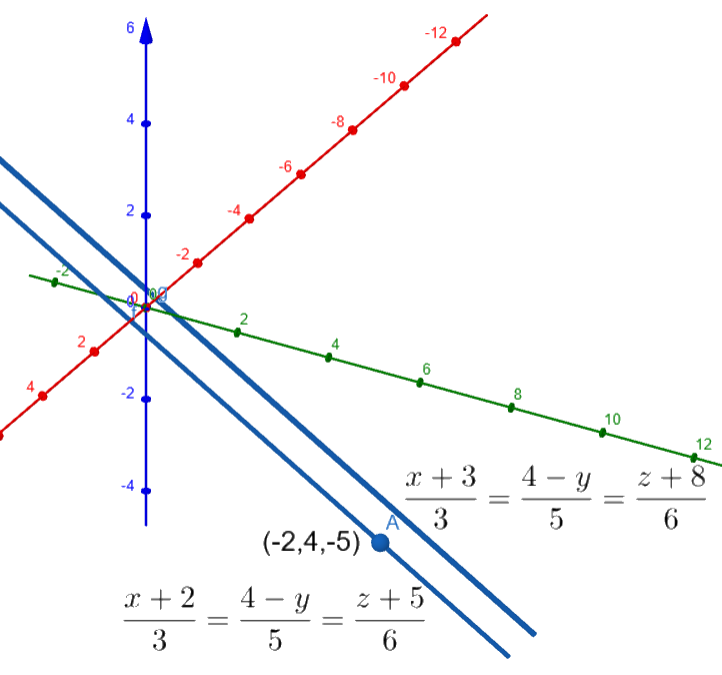
$\therefore$The equation of the required line is $\dfrac{x+2}{3}=\dfrac{4-y}{5}=\dfrac{z+5}{6}$.

Note: Students might commit a mistake while writing the directional ratios of $\dfrac{x+3}{3}=\dfrac{4-y}{5}=\dfrac{z+8}{6}$. The mistake that they do is by writing the value of the directional ratio corresponding to y as 5. We should remember that the general equation of the line has the coefficient of y as 1 but not -1. We should also take care if there are any coefficients other than 1 that are multiplied to the terms x, y, z in the equation. If there are any, we should divide by that co-efficient to make the coefficient as 1.