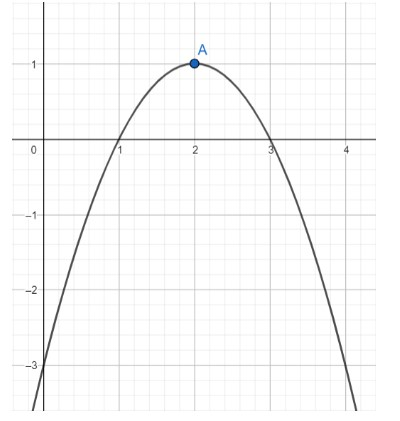
Question

Find the axis of symmetry of the parabola shown-

A. x = 1
B. x = 2.5
C. x = 3
D. None of these

Answer 1

Hint:In this question, we will first find the equation of the parabola using the graph. After that, we will use the concept that the axis of symmetry is along the axis of parabola. The general equation of a parabola is of the form-
${(x - h)^2} = 4a(y - k)$where h and k are the coordinates of the vertices.

Complete step-by-step answer:
From the graph, we can see that the parabola has its vertex at the point A, which has the coordinates $(2, 1)$. So the value of $h = 2$ and $k = 1$. The equation of the parabola can now be written as-
${(x - 2)^2} = 4a(y - 1)$
Now, we can see that the parabola cuts the x-axis at $(3, 0)$. We can substitute these values to get the value of a.
At (3, 0)-
$\begin{aligned} &{(3 - 2)^2} = 4a(0 - 1) \\\ &1 = - 4a \\\ &a; = - \dfrac{1}{4} \\\ \end{aligned}$

So, the equation of the parabola is-
${(x - 2)^2} = - 1(y - 1)$

The given parabola is a vertical parabola. The axis of vertical parabola is given by the formula-
$x - h = 0$
Substituting the value of h we get-
$x - 2 = 0$
$x = 2$
This is the axis of the parabola and the axis of symmetry. The correct option is D.

Note: If we observe the figure closely, we can see that the vertex of the parabola is at the point $(2, 1)$, and we draw an imaginary vertical line through A, we can get the axis of the parabola. The equation of this line is $x = 2$, as it is vertical and cuts the x-axis at $(2, 0)$.