Question

Find the axis of symmetry of $f\left( x \right) = 2{x^2} - 5x + 9$.
A $x = - \dfrac{5}{4}$
B $x = \dfrac{5}{4}$
C $x = - \dfrac{5}{2}$
D $x = \dfrac{5}{2}$

Answer 1

To find the axis of symmetry, we are given with the equation which is of the form, $a{x^2} + bx + c$, in which we need to apply the formula to find the axis of symmetry i.e., $x = - \dfrac{b}{{2a}}$, substituting the values of a and b we get the axis of symmetry.
Formula used:
Equation for the axis of symmetry:$x = - \dfrac{b}{{2a}}$
Here, $a$ and $b$ are coefficients.

Complete step by step answer:
Let us write the given data:
$f\left( x \right) = 2{x^2} - 5x + 9$
The given equation is of the form, $a{x^2} + bx + c$, in which
$a = 2$, $b = - 5$ and $c = 9$.
We know that, the equation for the axis of symmetry is given as:
$x = - \dfrac{b}{{2a}}$
Now, substitute the values in the formula we have:
$\Rightarrow x = - \dfrac{{ - 5}}{{2\left( 2 \right)}}$
Hence, the axis of symmetry of the given curve is:
$\Rightarrow x = \dfrac{5}{{2\left( 2 \right)}}$
$\Rightarrow x = \dfrac{5}{4}$

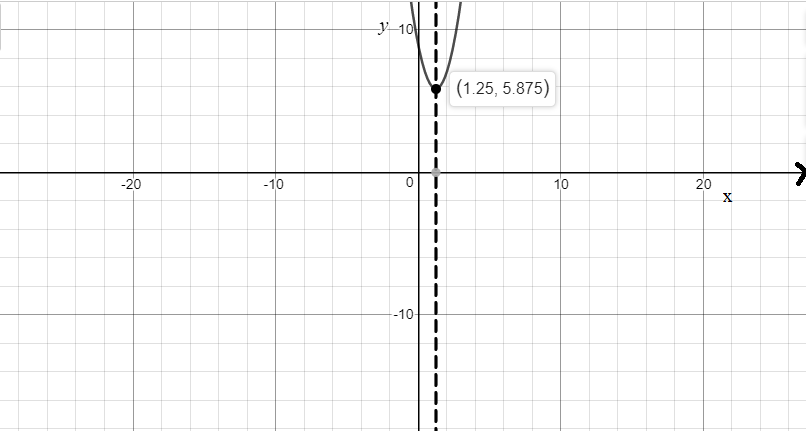
Therefore, the axis of symmetry passing through the vertex is vertical with equation $x = \dfrac{5}{4} = 1.25$.
So, the correct answer is “Option B”.

Note: We must note that the axis of symmetry of a parabola is a line about which the parabola is symmetrical. When the parabola is vertical, the line of symmetry is vertical and when a quadratic function is graphed in the coordinate plane, the resulting parabola and corresponding axis of symmetry are vertical.