Question

Find the area of the triangle formed by the points (8,4), (6,6) and (3,9).

Answer 1

Hint: Use the fact that the area of the triangle formed by the points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ and $C\left( {{x}_{3}},{{y}_{3}} \right)$ is given by $A=\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|$. Substitute the values of ${{x}_{1}},{{x}_{2}},{{x}_{3}},{{y}_{1}},{{y}_{2}}$ and ${{y}_{3}}$ and simplify and hence find the area of the triangle formed by the given points. Alternatively, use the fact that the area of the triangle formed by the points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ and $C\left( {{x}_{3}},{{y}_{3}} \right)$ is given by
$\dfrac{1}{2}\left| \begin{matrix} {{x}_{2}}-{{x}_{1}} & {{y}_{2}}-{{y}_{1}} \\\ {{x}_{3}}-{{x}_{1}} & {{y}_{3}}-{{y}_{1}} \\\ \end{matrix} \right|$.
Hence find the area of the triangle formed by the given points.

Complete step-by-step answer:
We have $A\equiv \left( 8,4 \right),B\equiv \left( 6,6 \right)$ and $C\equiv \left( 3,9 \right)$
We know that the area of the triangle formed by the points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ and $C\left( {{x}_{3}},{{y}_{3}} \right)$ is given by $A=\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|$.
Here ${{x}_{1}}=8,{{x}_{2}}=6,{{x}_{3}}=3,{{y}_{1}}=4,{{y}_{2}}=6$ and ${{y}_{3}}=9$
Hence the area of the triangle formed by these points is
$\dfrac{1}{2}\left| 8\left( 6-9 \right)+6\left( 9-4 \right)+3\left( 4-6 \right) \right|=\dfrac{1}{2}\left| -24+30-6 \right|=0$
Hence the area of the triangle formed by these points is 0

Note: Interpretation of area as 0: The area of the triangle formed by these points is 0 implies that these points are collinear and the triangle formed by these points is in fact a straight line.
This can be viewed graphically as shown:

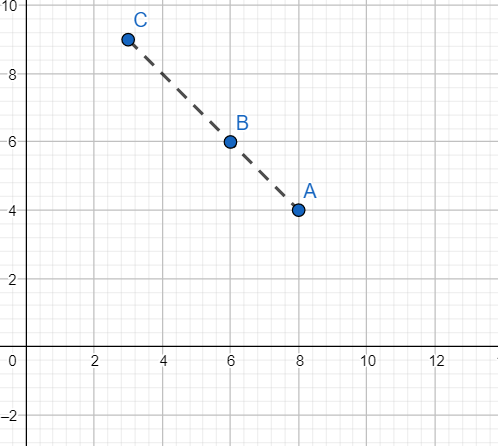
[ii] Alternative solution:
We know that the area of the triangle formed by the points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ and $C\left( {{x}_{3}},{{y}_{3}} \right)$ is given by
$\dfrac{1}{2}\left| \begin{matrix} {{x}_{2}}-{{x}_{1}} & {{y}_{2}}-{{y}_{1}} \\\ {{x}_{3}}-{{x}_{1}} & {{y}_{3}}-{{y}_{1}} \\\ \end{matrix} \right|$.
Hence the area of the triangle ABC is $\dfrac{1}{2}\left| \begin{matrix} 6-8 & 6-4 \\\ 3-8 & 9-4 \\\ \end{matrix} \right|=\dfrac{1}{2}\left| -2\times \left( 5 \right)-\left( -5 \right)\times 2 \right|=0$, which is the same as obtained above.