Question

Find the area of the triangle formed by the point (0,0) (4,0) (0,3)

Answer 1

Hint : We can find the area of the triangle by using the Distance Formula and the Area formula. Distance formulas will be used to find the individual distance of each side and then using the values obtained from the Distance formula we need to find the area of the triangle.
Distance Formula: $\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$
Area Formula: $\sqrt {s(s - {d_1})(s - {d_2})(s - {d_3})}$ where $s = \dfrac{{({d_1} + {d_2} + {d_3})}}{2}$

Complete step-by-step answer :

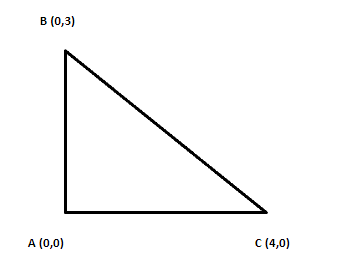
From the question we can see the triangle ABC is having the coordinates as A(0,0), B(4,0) & C(0,3). So, using the Distance Formula we will find the distance of side AB, BC & CA.
Distance of AB ( ${d_1}$ )
= $\sqrt {{{(4 - 0)}^2} + {{(0 - 0)}^2}}$
= $\sqrt {16}$
= 4 unit
Distance of BC ( ${d_2}$ )
= $\sqrt {{{(0 - 4)}^2} + {{(3 - 0)}^2}}$
= $\sqrt {{{( - 4)}^2} + {{(3)}^2}}$
= $\sqrt {16 + 9}$
= $\sqrt {25}$
= 5 unit
Distance of CA ( ${d_3}$ )
= $\sqrt {{{(0 - 0)}^2} + {{(3 - 0)}^2}}$
= $\sqrt 9$
= 3 unit
Using the individual distance values we will find the value of s.
So,
$s = \dfrac{{({d_1} + {d_2} + {d_3})}}{2}$
$s = \dfrac{{(4 + 5 + 3)}}{2}$
$s = \dfrac{{12}}{2}$
$s = 6$ unit
Using the Area Formula we will find the area of the triangle ABC.
So, area of triangle ABC
= $\sqrt {s(s - {d_1})(s - {d_2})(s - {d_3})}$
= $\sqrt {6(6 - 4)(6 - 5)(6 - 3)}$
= $\sqrt {6 \times 2 \times 1 \times 3}$
= $\sqrt {36}$
= 6 unit
Hence, the area of the triangle ABC will be 6 units.

Note : In the final values unit means it can be mm or cm or meter as per the question but since only points are given it's better to write only units. Generally, ‘s’ is known as the semi-perimeter of a triangle.