Question

Find the area of the shaded region in the following diagram

Answer 1

Hint : Formula for area of intersection of two circle is $A=r_{1}^{2}{{\cos }^{-1}}\left( \dfrac{{{d}_{1}}}{{{r}_{1}}} \right)-{{d}_{1}}\sqrt{r_{1}^{2}-d_{1}^{2}}+r_{2}^{2}{{\cos }^{-1}}\left( \dfrac{{{d}_{2}}}{{{r}_{2}}} \right)+{{d}_{2}}\sqrt{r_{2}^{2}-d_{2}^{2}}$
Here ${{r}_{1}}$ and ${{r}_{2}}$ are the radius of the first and second circle.
And ${{d}_{1}}$ , ${{d}_{2}}$ are the distance of radius from the line that pass-through intersection of two circles.

Complete step-by-step answer :

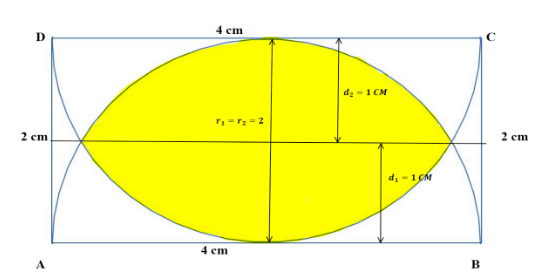
In the above diagram there are two semicircles and the semicircles are inside a rectangle.
So, we have two similar semicircles. The radius of the semi-circle is 2 centimetres. Hence here ${{r}_{1}}=2$ and ${{r}_{2}}=2$. As the distance from the line intersecting two circles is one centimetre that is ${{d}_{1}}={{d}_{2}}=1$.
Now using it in the formula for area
$A=r_{1}^{2}{{\cos }^{-1}}\left( \dfrac{{{d}_{1}}}{{{r}_{1}}} \right)-{{d}_{1}}\sqrt{r_{1}^{2}-d_{1}^{2}}+r_{2}^{2}{{\cos }^{-1}}\left( \dfrac{{{d}_{2}}}{{{r}_{2}}} \right)+{{d}_{2}}\sqrt{r_{2}^{2}-d_{2}^{2}}$
$\Rightarrow A={{2}^{2}}{{\cos }^{-1}}\left( \dfrac{1}{2} \right)-1\sqrt{{{2}^{2}}-{{1}^{2}}}+{{2}^{2}}{{\cos }^{-1}}\left( \dfrac{1}{2} \right)+1\sqrt{{{2}^{2}}-{{1}^{2}}}$
$A=4{{\cos }^{-1}}\left( \dfrac{1}{2} \right)-\sqrt{3}+4{{\cos }^{-1}}\left( \dfrac{1}{2} \right)+\sqrt{3}$
As we know ${{\cos }^{-1}}\left( \dfrac{1}{2} \right)$is $\dfrac{\pi }{3}$ using this in the equation
$\Rightarrow A=4\dfrac{\pi }{3}-\sqrt{3}+4\dfrac{\pi }{3}+\sqrt{3}=8\dfrac{\pi }{3}-0\sqrt{3}$
Hence, the area of the shaded region is $\left( 8\dfrac{\pi }{3} \right)c{{m}^{2}}$.

Note : Consider the following diagram

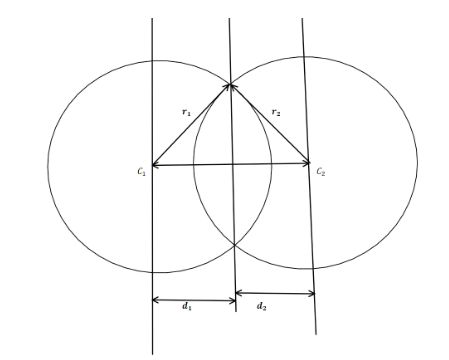
Here we have two circle with centre ${{c}_{1}}$ and ${{c}_{2}}$ and radius ${{r}_{1}}$ and ${{r}_{2}}$ and ${{d}_{1}}$ and ${{d}_{2}}$ are distance from the line that pass through intersection point of two circle .
And the formula for the area is
$A=r_{1}^{2}{{\cos }^{-1}}\left( \dfrac{{{d}_{1}}}{{{r}_{1}}} \right)-{{d}_{1}}\sqrt{r_{1}^{2}-d_{1}^{2}}+r_{2}^{2}{{\cos }^{-1}}\left( \dfrac{{{d}_{2}}}{{{r}_{2}}} \right)+{{d}_{2}}\sqrt{r_{2}^{2}-d_{2}^{2}}$
This formula can be used to find the intersecting area of any two circles.