Question

Find the area of the region \left\\{ \left( x,y \right):{{y}^{2}}\le 6ax\text{ and }{{x}^{2}}+{{y}^{2}}\le 16{{a}^{2}} \right\\} using method of integration.

Answer 1

We start solving the problem by finding the intersection point of the two curves. We then find the integrands and limits for the definite integral in order to find the area of the required region. We then use $\int{\sqrt{x}dx}=\dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}}+C$, $\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx}=\dfrac{x}{2}\left( \sqrt{{{a}^{2}}-{{x}^{2}}} \right)+\dfrac{{{a}^{2}}}{2}\left( {{\sin }^{-1}}\left( \dfrac{x}{a} \right) \right)+C$, $\int\limits_{a}^{b}{{{f}^{'}}\left( x \right)}=\left[ f\left( x \right) \right]_{a}^{b}=f\left( b \right)-f\left( a \right)$ and make necessary calculations required to get the area that lies above the x-axis. We multiply this with 2 to get the total area bounded by the curves.

Complete step-by-step solution:
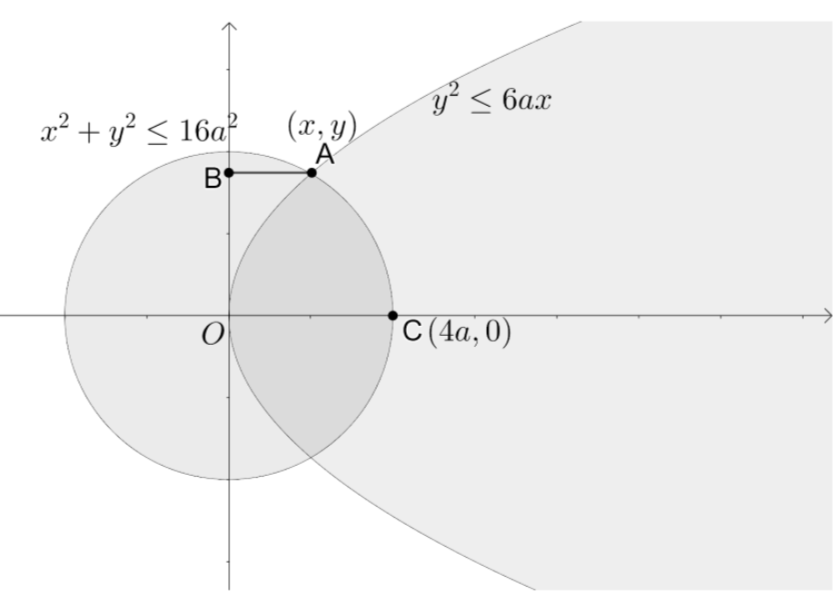
According to the problem, we need to find the area bounded by the region between the curves $\left( x,y \right):{{y}^{2}}\le 6ax\text{ and }{{x}^{2}}+{{y}^{2}}\le 16{{a}^{2}}$.
Let us find the intersection point of these two curves. Let us substitute ${{y}^{2}}=6ax$ in the curve${{x}^{2}}+{{y}^{2}}=16{{a}^{2}}$, as the intersection will only occur at the equality condition.

So, we get ${{x}^{2}}+6ax=16{{a}^{2}}$.
$\Rightarrow {{x}^{2}}+6ax-16{{a}^{2}}=0$.
$\Rightarrow {{x}^{2}}+8ax-2ax-16{{a}^{2}}=0$.
$\Rightarrow x\left( x+8a \right)-2a\left( x+8a \right)=0$.
$\Rightarrow \left( x-2a \right)\left( x+8a \right)=0$.
$\Rightarrow \left( x-2a \right)=0$ or $\left( x+8a \right)=0$.
$\Rightarrow x=2a$ or $x=-8a$.
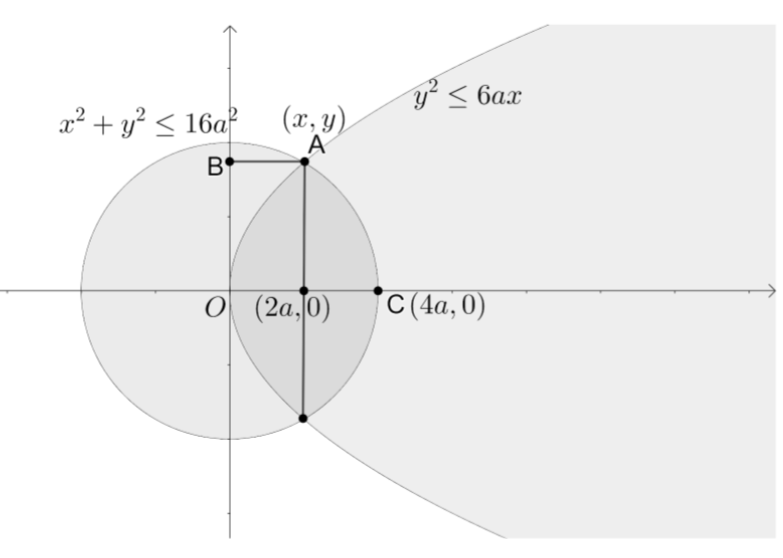
Since the curve ${{x}^{2}}+{{y}^{2}}\le 16{{a}^{2}}$ lies between $-4a$ and $4a$ we neglect $x=-8a$. So, the value of the x co-ordinate at the point of intersection is 2a.
We can see that the closed region between the two curves is between $x=0$ and $x=4a$. We can also see that the area between $x=0$ and $x=2a$ is bounded by the curve ${{y}^{2}}\le 6ax$ and the area between $x=2a$ and $x=4a$ is bounded by the curve ${{x}^{2}}+{{y}^{2}}\le 16{{a}^{2}}$.
So, let us write the equation of both curves in terms of $y=f\left( x \right)$. So, we get the equation of curve ${{y}^{2}}\le 6ax$ as $y\le \sqrt{6ax}$ and equation of the curve ${{x}^{2}}+{{y}^{2}}\le 16{{a}^{2}}$ as $y\le \sqrt{16{{a}^{2}}-{{x}^{2}}}$.
We know that the area bounded by the curve $f\left( x \right)$ between the values $x=a$ and $x=b$is defined by $\int\limits_{a}^{b}{f\left( x \right)dx}$, where $aSo, the required area (A) between the curves is$A=\int\limits_{0}^{2a}{\sqrt{6ax}dx}+\int\limits_{2a}^{4a}{\sqrt{16{{a}^{2}}-{{x}^{2}}}dx}$.$\Rightarrow A=\left( \sqrt{6a} \right)\int\limits_{0}^{2a}{\sqrt{x}dx}+\int\limits_{2a}^{4a}{\sqrt{{{\left( 4a \right)}^{2}}-{{\left( x \right)}^{2}}}dx}$. We know that$\int{\sqrt{x}dx}=\dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}}+C$,$\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx}=\dfrac{x}{2}\left( \sqrt{{{a}^{2}}-{{x}^{2}}} \right)+\dfrac{{{a}^{2}}}{2}\left( {{\sin }^{-1}}\left( \dfrac{x}{a} \right) \right)+C$and$\int\limits_{a}^{b}{{{f}^{'}}\left( x \right)}=\left[ f\left( x \right) \right]{a}^{b}=f\left( b \right)-f\left( a \right)$.$\Rightarrow A=\left( \sqrt{6a} \right)\left[ \dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right]{0}^{2a}+\left[ \dfrac{x}{2}\sqrt{{{\left( 4a \right)}^{2}}-{{x}^{2}}}+\dfrac{{{\left( 4a \right)}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{4a} \right) \right]{2a}^{4a}$.$\Rightarrow A=\left( \sqrt{6a} \right)\left[ \dfrac{2{{\left( 2a \right)}^{\dfrac{3}{2}}}}{3}-\dfrac{2{{\left( 0 \right)}^{\dfrac{3}{2}}}}{3} \right]+\left[ \dfrac{x}{2}\sqrt{{{\left( 4a \right)}^{2}}-{{x}^{2}}}+\dfrac{{{\left( 4a \right)}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{4a} \right) \right]{2a}^{4a}$.$\Rightarrow A=\left( \sqrt{6a} \right)\left[ \dfrac{2\left( 2\sqrt{2} \right){{a}^{\dfrac{3}{2}}}}{3}-0 \right]+\left[ \dfrac{x}{2}\sqrt{{{\left( 4a \right)}^{2}}-{{x}^{2}}}+\dfrac{{{\left( 4a \right)}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{4a} \right) \right]{2a}^{4a}$.$\Rightarrow A=\left( \sqrt{6a} \right)\left[ \dfrac{2\left( 2\sqrt{2} \right){{a}^{\dfrac{3}{2}}}}{3} \right]+\left[ \dfrac{x}{2}\sqrt{{{\left( 4a \right)}^{2}}-{{x}^{2}}}+\dfrac{{{\left( 4a \right)}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{4a} \right) \right]{2a}^{4a}$.$\Rightarrow A=\left[ \dfrac{8\sqrt{3}{{a}^{2}}}{3} \right]+\left[ \dfrac{x}{2}\sqrt{{{\left( 4a \right)}^{2}}-{{x}^{2}}}+\dfrac{{{\left( 4a \right)}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{4a} \right) \right]_{2a}^{4a}$.$\Rightarrow A=\left[ \dfrac{8\sqrt{3}{{a}^{2}}}{3} \right]+\left( \dfrac{4a}{2}\sqrt{{{\left( 4a \right)}^{2}}-{{\left( 4a \right)}^{2}}}+\dfrac{{{\left( 4a \right)}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{4a}{4a} \right) \right)-\left( \dfrac{2a}{2}\sqrt{{{\left( 4a \right)}^{2}}-{{\left( 2a \right)}^{2}}}+\dfrac{{{\left( 4a \right)}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{2a}{4a} \right) \right)$.$\Rightarrow A=\left[ \dfrac{8\sqrt{3}{{a}^{2}}}{3} \right]+\left( 2a\sqrt{16{{a}^{2}}-16{{a}^{2}}}+\dfrac{16{{a}^{2}}}{2}{{\sin }^{-1}}\left( 1 \right) \right)-\left( a\sqrt{16{{a}^{2}}-4{{a}^{2}}}+\dfrac{16{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{1}{2} \right) \right)$.$\Rightarrow A=\left[ \dfrac{8\sqrt{3}{{a}^{2}}}{3} \right]+\left( 2a\sqrt{0}+8{{a}^{2}}\left( \dfrac{\pi }{2} \right) \right)-\left( a\sqrt{12{{a}^{2}}}+8{{a}^{2}}\left( \dfrac{\pi }{6} \right) \right). $$\Rightarrow A=\left[ \dfrac{8\sqrt{3}{{a}^{2}}}{3} \right]+\left( 4{{a}^{2}}\pi \right)-\left( 2\sqrt{3}{{a}^{2}}+\dfrac{4{{a}^{2}}\pi }{3} \right)$$. $$\Rightarrow A=\dfrac{8\sqrt{3}{{a}^{2}}}{3}-2\sqrt{3}{{a}^{2}}+4{{a}^{2}}\pi -\dfrac{4{{a}^{2}}\pi }{3}$$. $$\Rightarrow A=\dfrac{8\sqrt{3}{{a}^{2}}-6\sqrt{3}{{a}^{2}}}{3}+\dfrac{12{{a}^{2}}\pi -4{{a}^{2}}\pi }{3}$$. $$\Rightarrow A=\dfrac{2\sqrt{3}{{a}^{2}}}{3}+\dfrac{8{{a}^{2}}\pi }{3}$$. $$\Rightarrow A=\dfrac{2{{a}^{2}}}{3}\left( \sqrt{3}+4\pi \right)$$ ---(1). But we here get the area that lies only above the x-axis. In order to get the area below the x-axis, we need to multiply equation (1) with 2. \Rightarrow 2A=\dfrac{4{{a}^{2}}}{3}\left( \sqrt{3}+4\pi \right)$. So, we have found the area of the region as$\dfrac{4{{a}^{2}}}{3}\left( \sqrt{3}+4\pi \right)$.$\therefore$The area of the region bounded by the curves$\left( x,y \right):{{y}^{2}}\le 6ax\text{ and }{{x}^{2}}+{{y}^{2}}\le 16{{a}^{2}}$is$\dfrac{4{{a}^{2}}}{3}\left( \sqrt{3}+4\pi \right)$.

Note: Here the integrands we have used give only the positive values for y, which is the reason why we get the area of the region that lies above the x-axis. Because the positive y-axis lies above the x-axis. Whenever we are asked to find areas of two intersecting functions, we need to find the area of the closed bounded region. If those are not intersecting, limits of integration have to be given in order to get the area bounded between them.