Question
Question: Find the area of the region \[\left\\{ \left( x,y \right):{{x}^{2}}+{{y}^{2}}\le 1\le x+y \right\\}\...
Find the area of the region \left\\{ \left( x,y \right):{{x}^{2}}+{{y}^{2}}\le 1\le x+y \right\\}.
Solution
First, from the given expression / conditions, find 2 curves which we need to find the area. Next by using elimination method find the points of intersection of the curves. By looking at their equations, use normal co – ordinate geometry knowledge to find their shapes. Draw the curves together on a graph. By using their diagrams mark the area which is common in both of them. Now, integrate the curves to find the area and subtract the extra area to get the area which is in common to both curves.
Complete step-by-step answer:
Elimination method:
First write 2 curve equations which you need to solve to find intersection points. Then try to convert one variable in terms of another variable by using any one of the equations. Now substitute this variable in terms of others into the remaining equation. Now the remaining equation turns into an equation of one variable. By normal geometry find the variable. Using previous relations, find the other variable. Thus, you get the intersection point(s).
The expression given in the question is written as:
\Rightarrow $$$${{x}^{2}}+{{y}^{2}}\le 1\le x+y
From this expression we can derive 2 equations such as:
⇒x2+y2≤1 1≤x+y
By general coordinate geometry we say that the first curve is a circle and the second curve is a straight line.
For finding intersection point (s) we write them as: -
⇒ x2+y2=1 - (1)
\Rightarrow $$$$x+y=1 - (2)
From equation (2) by subtracting x on both sides, we get:
⇒y=1−x - (3)
By substituting this y value into equation (1), we get:
⇒x2+(1−x)2=1
We know, (a−b)2=a2−2ab+b2, by using this to above equation, we get:
⇒x2+1−2x+x2=1
By subtracting 1 on both sides and then simplifying, we get:
⇒2x2−2x=0
By dividing with 2 on both sides and taking x common, we get:
⇒x(x−1)=0
By above we can say roots of equation are, x = 0, 1
By substituting these x values into equation (3)
If x = 0, y = 1 – 0 = 1; If x = 1, y = 1 – 1 = 0.
From above we get the intersection points as (0, 1); (1, 0).
Next we will draw the curves and mark the area.
Curves: -
x2+y2=1
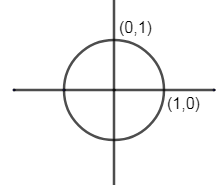
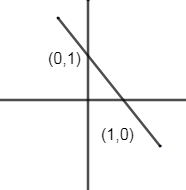
x+y=1
Areas: -
x2+y2≤1
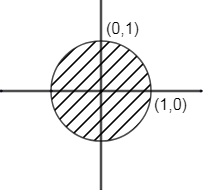
x+y≥1
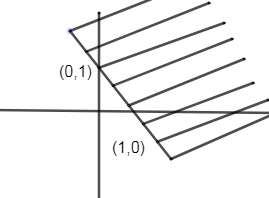
Combining both areas, we get:
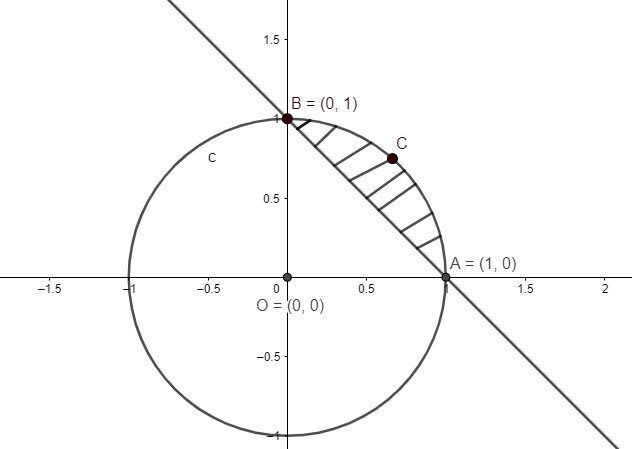
We have done areas ≤ means area bounded inside and ≥ means area including the point to outside of the curve.
As you can see from the above diagram, we need the area ACB.
So, if we subtract the area integrated at intersection points of 2 curves we get the required area.
Curve 1: - x2+y2=1
By subtracting x2 on both sides and applying square root on both sides we get:
⇒y=1−x2 - (4)
Curve 2: y=1−x - (5)
Area bounded between 2 curves f(x), g(x) at intersection points (x1,y1), (x2,y2) is given by,
Area = x1∫x2f(x)−g(x)dx - (7), where f(x) is above g(x).
Here the circle is above the straight line; and from diagrams we can say area of circle from (0, 1) to (1, 0) – area of straight line from (0, 1) to (1, 0) we get the required area.
So, from equation (4) and equation (5), we say:
⇒f(x)=1−x2;g(x)=1−x
By substituting these into equation (7), we get:
Area = 0∫11−x2−(1−x)dx
By simplifying the above expression, we can write it as:
Area = 0∫11−x2dx−0∫11dx+0∫1xdx
By basic integration formulae, we can say:
