Question

Find the area of the region \left\\{ \left( x,y \right):0\le y\le \left( {{x}^{2}}+1 \right),0\le y\le \left( x+1 \right),0\le x\le 2 \right\\} .

Answer 1

Hint: For solving this question, first we will plot the given curves on the same $x-y$ plane. Then, we will find the desired region whose area is asked in the question. After that, we will divide the given region into two regions, and find their area separately by taking an elementary vertical strip of width $dx$ and try to write its height in terms of the variable $x$ . Then, we will write the area of the elementary in terms of $x$ and $dx$ by multiplying its height and width. And finally, we will integrate the area of the elementary strip with suitable limits to get the area of each part. Then, we will add them to get the total area of the desired region.

Complete step-by-step answer:
Given:
We have to find the area of the region \left\\{ \left( x,y \right):0\le y\le \left( {{x}^{2}}+1 \right),0\le y\le \left( x+1 \right),0\le x\le 2 \right\\} .
Now, before we proceed we should plot the curve $y=0$ , $y={{x}^{2}}+1$ , $y=x+1$ , $x=0$ and $x=2$ on the same $x-y$ plane, then we will figure out the region \left\\{ \left( x,y \right):0\le y\le \left( {{x}^{2}}+1 \right),0\le y\le \left( x+1 \right),0\le x\le 2 \right\\} . For more clarity, look at the figure given below:

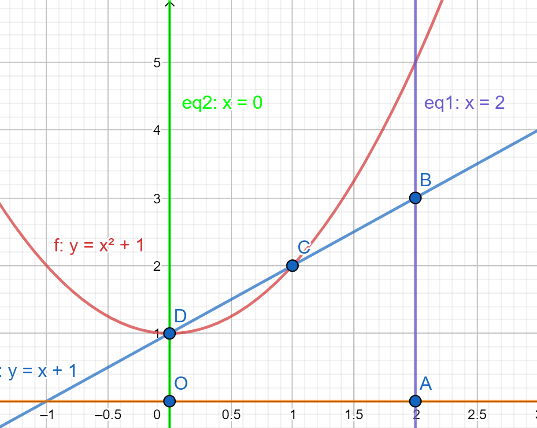
In the above figure, we have to find the area of the region OABCD and while moving from point C to D we should follow the curve $y={{x}^{2}}+1$ .
Now, the coordinates of the point $A\equiv (2,0)$ and for coordinates of the point B, we will put $x=2$ in the equation $y=x+1$ . Then,
$\begin{aligned} & {{y}_{B}}=x+1 \\\ & \Rightarrow {{y}_{B}}=2+1 \\\ & \Rightarrow {{y}_{B}}=3 \\\ \end{aligned}$
Now, from the above result, we can say that coordinates of the point $B\equiv (2,3)$ and for the coordinates of D and C, we have to solve the equation $y={{x}^{2}}+1$ and $y=x+1$ . Then,
$\begin{aligned} & y={{x}^{2}}+1=x+1 \\\ & \Rightarrow {{x}^{2}}+1=x+1 \\\ & \Rightarrow {{x}^{2}}-x=0 \\\ & \Rightarrow x\left( x-1 \right)=0 \\\ & \Rightarrow x=0,1 \\\ \end{aligned}$
Now, from the above result and the figure, we can say that to get the coordinates of point D we should put $x=0$ and to get the coordinates of point C we should put $x=1$ in the equation $y=x+1$ . Then,
$\begin{aligned} & {{y}_{D}}=x+1 \\\ & \Rightarrow {{y}_{D}}=1 \\\ & {{y}_{C}}=x+1 \\\ & \Rightarrow {{y}_{C}}=1+1 \\\ & \Rightarrow {{y}_{C}}=2 \\\ \end{aligned}$
Now, from the above result, we conclude that coordinates of points $D\equiv (0,1)$ and $C\equiv (1,2)$ .
Now, we draw a line segment CE perpendicular to $x-axis$ from point C. For more clarity, look at the figure given below:

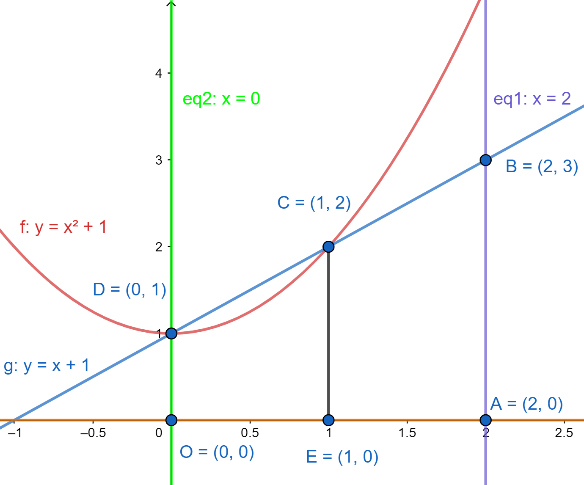
Now, we will first find the area of the region OECD, and region EABC separately and then we will add them to get the total area of the region OABCD.
Area of the region OECD:
Now, we take an elementary vertical strip at $x$ of width $dx$ . For more clarity, look at the figure given below:

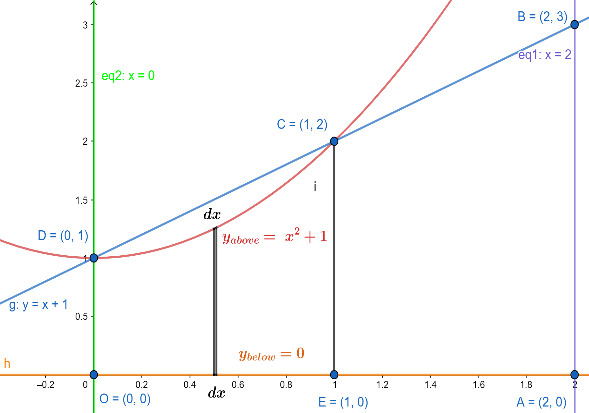
Now, to find the height of the elementary strip, we should subtract the ${{y}_{above}}={{x}^{2}}+1$ and ${{y}_{below}}=0$ . Then,
Height of the elementary strip $={{y}_{above}}-{{y}_{below}}={{x}^{2}}+1$ .
Now, as we know, the width of the elementary strip is $dx$ . So, the area of the elementary strip will be height multiplied by width. Then,
Area of the elementary strip $=dA=\left( {{x}^{2}}+1 \right)dx$ .
Now, to get the total area of the region OECD, we should add the area of such elementary strips from $x=0$ to $x=1$ so, to get the desired area we should integrate the expression $\left( {{x}^{2}}+1 \right)dx$ from $x=0$ to $x=1$ . Then,
Area of the desired region $=\int\limits_{0}^{1}{\left( {{x}^{2}}+1 \right)dx}$ .
Now, we will use the formula $\int{{{x}^{n}}dx=\dfrac{{{x}^{n+1}}}{n+1}+c}$ to integrate the above integral. Then,
$\begin{aligned} & \int\limits_{0}^{1}{\left( {{x}^{2}}+1 \right)dx} \\\ & \Rightarrow \left[ \dfrac{{{x}^{3}}}{3}+x \right]_{0}^{1} \\\ & \Rightarrow \left[ \dfrac{{{1}^{3}}}{3}+1-0 \right] \\\ & \Rightarrow \dfrac{1}{3}+1 \\\ & \Rightarrow \dfrac{4}{3} \\\ \end{aligned}$
Now, from the above result, we conclude that the area of the region OECD will be $\dfrac{4}{3}\text{ sq}\text{.units}$ .

Area of the region EABC:
Now, we take an elementary vertical strip at $x$ of width $dx$ . For more clarity, look at the figure given below:

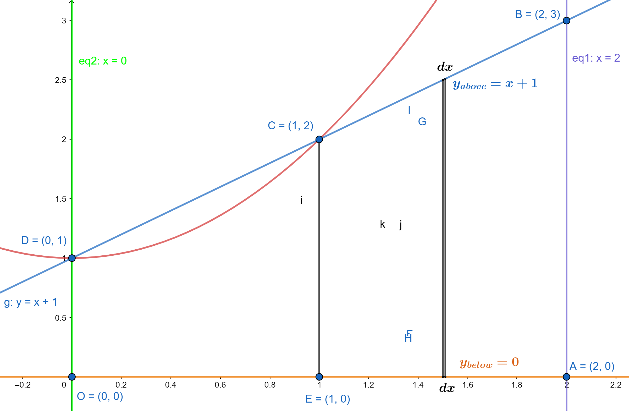
Now, to find the height of the elementary strip, we should subtract the ${{y}_{above}}=x$ and ${{y}_{below}}=0$ . Then,
Height of the elementary strip $={{y}_{above}}-{{y}_{below}}=x$ .
Now, as we know, the width of the elementary strip is $dx$ . So, the area of the elementary strip will be height multiplied by width. Then,
Area of the elementary strip $=dA=\left( x \right)dx$ .
Now, to get the total area of the region EABC, we should add the area of such elementary strips from $x=1$ to $x=2$ so, to get the desired area we should integrate the expression $\left( x \right)dx$ from $x=1$ to $x=2$ . Then,
Area of the desired region $=\int\limits_{1}^{2}{\left( x \right)dx}$ .
Now, we will use the formula $\int{{{x}^{n}}dx=\dfrac{{{x}^{n+1}}}{n+1}+c}$ to integrate the above integral. Then,
$\begin{aligned} & \int\limits_{1}^{2}{\left( x \right)dx} \\\ & \Rightarrow \left[ \dfrac{{{x}^{2}}}{2} \right]_{1}^{2} \\\ & \Rightarrow \left[ \dfrac{4}{2}-\dfrac{1}{2} \right] \\\ & \Rightarrow \dfrac{3}{2} \\\ \end{aligned}$
Now, from the above result, we conclude that the area of the region EABC will be $\dfrac{3}{2}\text{ sq}\text{.units}$ .
Now, we will add the area of the region OECD and region EABC to get the total area of the region OABCD. Then,
Total area of the region OABCD $=\dfrac{4}{3}+\dfrac{3}{2}=\dfrac{17}{6}\text{ sq}\text{.units}$ .
Now, from the above result, we conclude that area of the desired region will be $\dfrac{17}{6}\text{ sq}\text{.units}\approx 2.833\text{ sq}\text{.units}$ .
Thus, the area of the region \left\\{ \left( x,y \right):0\le y\le \left( {{x}^{2}}+1 \right),0\le y\le \left( x+1 \right),0\le x\le 2 \right\\} will be equal to $\text{2}\text{.833 sq}\text{.units}$ approximately.

Note: Here, the student should first plot the given curves carefully and then find the desired region whose area is asked in the question and proceed in a stepwise manner. Then, we should be careful while writing the dimensions of the elementary strip and for that, we should take help from the plot of the given curves. Moreover, though the integration part is very easy, we should take upper and lower limits correctly, to get the correct answer and whenever we get stuck at some point we should see the plot of the given curves and use the basic concepts of integral calculus.