Question

Find the area of the region included between the parabolas ${{y}^{2}}=4ax$ and ${{x}^{2}}=4ay$ , where $a>0$ .

Answer 1

For solving this question, first we will plot the given curves on the same $x-y$ plane. Then, we will find the desired region whose area is asked in the question. After that, we will solve the given equations and find the coordinates of the intersection points. Then, we will take an elementary horizontal strip of width $dy$ and try to write its length in terms of the variable $y$ . Then, we will write the area of the elementary in terms of $y$ and $dy$ by multiplying its length and width. And finally, we will integrate the area of the elementary strip with suitable limits to get the total area of the given region.

Complete step-by-step answer:
Given,
We have to find the area of the region included between the parabolas ${{y}^{2}}=4ax$ and ${{x}^{2}}=4ay$ , where $a>0$ .
Now, before we proceed we should plot the curves ${{y}^{2}}=4ax$ and ${{x}^{2}}=4ay$ on the same $x-y$ plane. For more clarity, look at the figure given below:

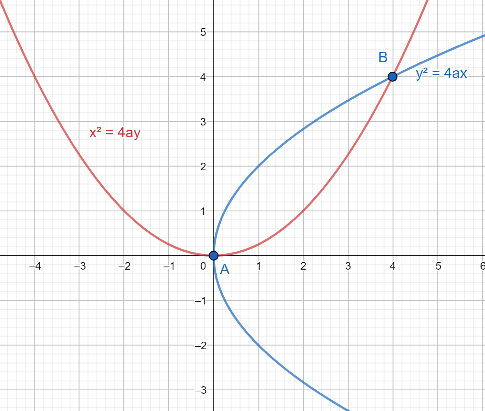
In the above figure, we have to find the area of the region bounded by the curve ${{y}^{2}}=4ax$ and the line ${{x}^{2}}=4ay$ .
Now, from the above figure, we can say that for the coordinates of points A and B we should equate the equations ${{y}^{2}}=4ax$ and ${{x}^{2}}=4ay$ . Then,
$\begin{aligned} & {{x}^{2}}=4ay \\\ & \Rightarrow y=\dfrac{{{x}^{2}}}{4a} \\\ \end{aligned}$
Now, we put $y=\dfrac{{{x}^{2}}}{4a}$ in the equation ${{y}^{2}}=4ax$ . Then,
$\begin{aligned} & {{y}^{2}}=4ax \\\ & \Rightarrow {{\left( \dfrac{{{x}^{2}}}{4a} \right)}^{2}}=4ax \\\ & \Rightarrow \dfrac{{{x}^{4}}}{16{{a}^{2}}}=4ax \\\ & \Rightarrow \dfrac{{{x}^{4}}}{16{{a}^{2}}}-4ax=0 \\\ \end{aligned}$
Taking x as common in the left hand side of the above equation we get,
$\Rightarrow x\left( \dfrac{{{x}^{3}}}{16{{a}^{2}}}-4a \right)=0$
Equating x to 0 and the expression written in the bracket to 0 we get,
$\begin{aligned} & x=0; \\\ & \dfrac{{{x}^{3}}}{16{{a}^{2}}}-4a=0 \\\ \end{aligned}$
Solving $\dfrac{{{x}^{3}}}{16{{a}^{2}}}-4a=0$ we get,
${{x}^{3}}=64{{a}^{3}}$
Taking cube root on both the sides we get,
$x=4a$
Now, from the above result and the figure, we can say that to get the coordinates of point A we should put $x=0$ and to get the coordinates of point B we should put $x=4a$ in the equation ${{y}^{2}}=4ax$ . Then,
${{y}_{A}}^{2}=4a{{x}_{A}}$
Substituting ${{x}_{A}}=0$ in the above equation we get,
$\begin{aligned} & \Rightarrow {{y}^{2}}_{A}=4\times a\times 0 \\\ & \Rightarrow {{y}_{A}}=0 \\\ \end{aligned}$
${{y}_{B}}^{2}=4a{{x}_{B}}$
Substituting ${{x}_{B}}=4a$ in the above equation we get,
$\begin{aligned} & {{y}_{B}}^{2}=4a\left( 4a \right) \\\ & \Rightarrow {{y}_{B}}^{2}=16{{a}^{2}} \\\ \end{aligned}$
Taking square root on both the sides we get,
${{y}_{B}}=4a$
Now, from the above result, we conclude that coordinates of points $A\equiv (0,0)$ and $B\equiv (4a,4a)$ .
Now, we take an elementary horizontal strip at $y$ of width $dy$ . For more clarity, look at the figure given below:

Now, to find the length of the elementary strip, we should subtract the ${{x}_{right}}=\sqrt{4ay}$ and ${{x}_{left}}=\dfrac{{{y}^{2}}}{4a}$ . Then,
length of the elementary strip $={{x}_{right}}-{{x}_{left}}=\sqrt{4ay}-\dfrac{{{y}^{2}}}{4a}={{y}^{\dfrac{1}{2}}}\sqrt{4a}-\dfrac{{{y}^{2}}}{4a}$ .
Now, as we know, the width of the elementary strip is $dy$ . So, the area of the elementary strip will be length multiplied by width. Then,
Area of the elementary strip $=dA=\left( {{y}^{\dfrac{1}{2}}}\sqrt{4a}-\dfrac{{{y}^{2}}}{4a} \right)dy$ .
Now, to get the total area of the region, we should add the area of such elementary strips from $y=0$ to $y=4a$ so, to get the desired area we should integrate the expression $\left( {{y}^{\dfrac{1}{2}}}\sqrt{4a}-\dfrac{{{y}^{2}}}{4a} \right)dy$ from $y=0$ to $y=4a$ . Then,
Area of the desired region $=\int\limits_{0}^{4a}{\left( {{y}^{\dfrac{1}{2}}}\sqrt{4a}-\dfrac{{{y}^{2}}}{4a} \right)dy}$ .
Now, we will use the formula $\int{{{y}^{n}}dy=\dfrac{{{y}^{n+1}}}{n+1}+c}$ to integrate the above integral. Then,

& \int\limits_{0}^{4a}{\left( {{y}^{\dfrac{1}{2}}}\sqrt{4a}-\dfrac{{{y}^{2}}}{4a} \right)dy} \\\ & \Rightarrow \left[ \dfrac{{{y}^{\dfrac{3}{2}}}}{\dfrac{3}{2}}\times \sqrt{4a}-\dfrac{{{y}^{3}}}{12a} \right]_{0}^{4a} \\\ \end{aligned}$$ Applying the upper and lower limit in the result of integration we get, $$\begin{aligned} & \Rightarrow \left[ \left( \dfrac{2{{\left( 4a \right)}^{\dfrac{3}{2}}}\times {{\left( 4a \right)}^{\dfrac{1}{2}}}}{3}-\dfrac{{{\left( 4a \right)}^{3}}}{12a} \right)-\left( 0 \right) \right] \\\ & \Rightarrow \left[ \dfrac{2\times 16{{a}^{2}}}{3}-\dfrac{64{{a}^{3}}}{12a} \right] \\\ & \Rightarrow \left[ \dfrac{32{{a}^{2}}}{3}-\dfrac{16{{a}^{3}}}{3} \right] \\\ & \Rightarrow \dfrac{16{{a}^{3}}}{3} \\\ \end{aligned}$$ Now, from the above result, we conclude that the desired area will be $\dfrac{16{{a}^{3}}}{3}\text{ sq}\text{.units}$ . Thus, the area of the region included between the parabolas ${{y}^{2}}=4ax$ and ${{x}^{2}}=4ay$ , where $a>0$ will be equal to $\dfrac{16{{a}^{3}}}{3}\text{ sq}\text{.units}$ . **Note:** Here, the student should first plot the given curves carefully and then find the desired region whose area is asked in the question and proceed in a stepwise manner. Then, we should be careful while writing the dimensions of the elementary strip and for that, we should take help from the plot of the given curves. Moreover, for easy calculation, we should take horizontal elementary strips, and we should take upper and lower limits correctly, to get the correct answer and whenever we got stuck at some point we should see the plot of the given curves and use the basic concepts of integral calculus. And we should remember this result for solving some objective questions quickly.