Question

Find the area of the region in the first quadrant enclosed by x-axis, line ${\text{x = }}\sqrt 3 {\text{y}}$ and the circle ${x^2} + {y^2} = 4$.

Answer 1

Since they have told to find the area of the region enclosed by x-axis, line ${\text{x = }}\sqrt 3 {\text{y}}$ and the circle ${x^2} + {y^2} = 4$, first try to construct the diagram using all the information given and try to find the region enclosed by this lines and curves. Then use a suitable strip to calculate the area of the required region and then integrate all over.

Complete step by step solution:
Since we have to find the area which is enclosed in the first quadrant and enclosed by x-axis, line ${\text{x = }}\sqrt 3 {\text{y}}$ and the circle ${x^2} + {y^2} = 4$, we will first try to construct the given lines and circle as following

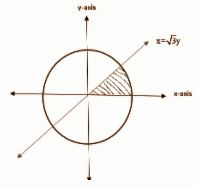
Here the shaded portion shows the area we have to calculate.
Let us start. We will try to use the polar coordinates to solve this sum and find the area.
Since we have been given that ${x^2} + {y^2} = 4$, comparing it with${x^2} + {y^2} = {r^2}$in the polar form we get $r = \pm 2$. But since $r$is radius, $r = 2$.
Now let us try to find the angle between the line ${\text{x = }}\sqrt 3 {\text{y}}$and x-axis
$x = \sqrt 3 y \\\ \Rightarrow y = \dfrac{1}{{\sqrt 3 }}x \\\$
That implies that the slope of the line ${\text{x = }}\sqrt 3 {\text{y}}$ is $\dfrac{1}{{\sqrt 3 }}$.
Therefore to find the angle using slope we use the formula
$\tan \theta = {\text{slope}} \\\ \Rightarrow {\text{tan}}\theta {\text{ = }}\dfrac{1}{{\sqrt 3 }} \\\ \Rightarrow \theta = {\tan ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right) \\\ \Rightarrow \theta = \dfrac{\pi }{6} \\\$
Therefore the angle between the line ${\text{x = }}\sqrt 3 {\text{y}}$ and x-axis is $\dfrac{\pi }{6}$
Let us construct a strip as shown in the figure so that it will help us calculate the area

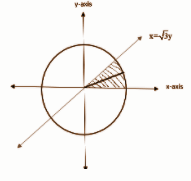
We will first try to find the area of the strip.
Let $d{\text{A}}$ be the area of the strip and $d\theta$ be the angle between the strip.
Therefore we get $d{\text{A = }}\dfrac{1}{2}r \times rd\theta$
Since $r = 2$ we get
$d{\text{A = }}\dfrac{1}{2} \times 2 \times 2d\theta \\\ = 2d\theta \\\$
Integrating the above equation we get,
${\text{A = }}\int\limits_0^{\dfrac{\pi }{6}} {2d\theta } \\\ = 2\int\limits_0^{\dfrac{\pi }{6}} {d\theta } \\\ = 2\left[ \theta \right]_0^{\dfrac{\pi }{6}} \\\ = 2\left[ {\dfrac{\pi }{6} - 0} \right] \\\ = \dfrac{\pi }{3} \\\$
Hence we get our desired area which is enclosed by x-axis, line ${\text{x = }}\sqrt 3 {\text{y}}$ and the circle ${x^2} + {y^2} = 4$ in the first quadrant as $\dfrac{\pi }{3}$ respectively.

Note:
Whenever we have been given a sum where area is told to be found and there is a curve present there, especially a circle, try to solve the sum by polar coordinates rather than by cartesian form, as using polar coordinates will give us results faster and easier than by using cartesian form. Also always construct the diagram.