Question

Find the area of the region enclosed in the first quadrant by the x-axis, the line $y=x$ and the circle ${{x}^{2}}+{{y}^{2}}=32$.

Answer 1

To solve this question, we should draw the diagram and indicate the points of intersection and points of change in the required area. By solving the equations $y=x$ and ${{x}^{2}}+{{y}^{2}}=32$ and the condition is that the area is in first quadrant, we get the point (4, 4) as the intersection point. The area we are asked is the area enclosed by the three curves y = x, y = 0 and ${{x}^{2}}+{{y}^{2}}=32$. The graph will look like the picture below.

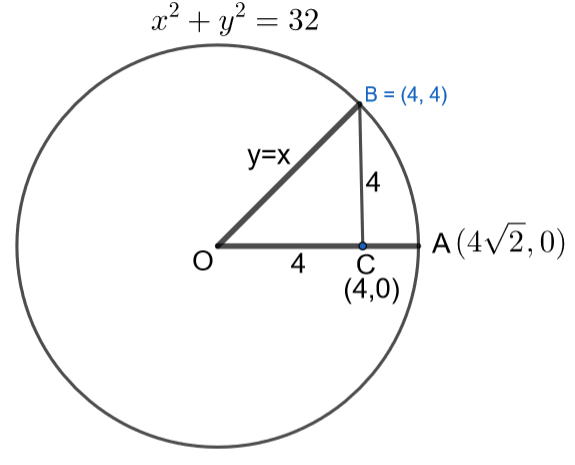
We are asked to find the area of the region OABO. To calculate this, we should divide the area into two parts. The two parts are OBCO and BCAB. We can infer from the diagram that the area OBCO is a right angled triangle with sides other than hypotenuse as 4, 4. The area is given by $Area=\dfrac{1}{2}\times 4\times 4=8$. The area of BCAB can be calculated using the integration. The area under bounded by the curves $y=f\left( x \right),x=a,x=b,y=0$ is given by $\int\limits_{x=a}^{x=b}{f\left( x \right)}dx$. Using this, we can calculate the area of the region where $y=f\left( x \right)=\sqrt{32-{{x}^{2}}}$, $x=a=4$, $x=b=4\sqrt{2}$. The integral becomes$Are{{a}_{2}}=\int\limits_{4}^{4\sqrt{2}}{\sqrt{32-{{x}^{2}}}dx}$. To solve this integral, we should substitute$x=\sqrt{32}\sin \theta \Rightarrow dx=\sqrt{32}\cos \theta d\theta$. The total required area is the area of the sum of both the areas.

Complete step by step answer:
The given equation is a circle with a radius $r=\sqrt{32}$ unit.
By substituting y = x in ${{x}^{2}}+{{y}^{2}}=32$, we get
$\begin{aligned} & {{x}^{2}}+{{x}^{2}}=32 \\\ & {{x}^{2}}=16 \\\ & x=\pm 4 \\\ \end{aligned}$
As the region is in the first quadrant, we get x = 4.
We can divide the area into two regions. The two regions are OBCO and BCAB.
We can infer that the figure OBCO is a right angled isosceles triangle with side = 4 units.
The area of the isosceles triangle = $\dfrac{1}{2}\times 4\times 4=8$.
We can calculate the area of BCAB using the integration.
We know that the area under bounded by the curves $y=f\left( x \right),x=a,x=b,y=0$ is given by $\int\limits_{x=a}^{x=b}{f\left( x \right)}dx$.
Using this, we can calculate the area of the region where
$y=f\left( x \right)=\sqrt{32-{{x}^{2}}}$, $x=a=4$, $x=b=4\sqrt{2}$.
The integral becomes$Are{{a}_{2}}=\int\limits_{4}^{4\sqrt{2}}{\sqrt{32-{{x}^{2}}}dx}$.
To solve this integral, we should substitute
$\begin{aligned} & x=\sqrt{32}\sin \theta \\\ & dx=\sqrt{32}\cos \theta d\theta \\\ \end{aligned}$.
The limits change to
$\begin{aligned} & {{x}_{1}}=4=\sqrt{32}\sin \theta \\\ & \sin \theta =\dfrac{4}{4\sqrt{2}}=\dfrac{1}{\sqrt{2}} \\\ & {{\theta }_{1}}=\dfrac{\pi }{4} \\\ \end{aligned}$
$\begin{aligned} & {{x}_{2}}=4\sqrt{2}=\sqrt{32}\sin \theta \\\ & \sin \theta =\dfrac{4\sqrt{2}}{4\sqrt{2}}=1 \\\ & {{\theta }_{2}}=\dfrac{\pi }{2} \\\ \end{aligned}$
Substituting them in the integral, we get
$\begin{aligned} & Are{{a}_{2}}=\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}{\sqrt{32-{{\left( \sqrt{32}\sin \theta \right)}^{2}}}\sqrt{32}\cos \theta d\theta } \\\ & =\sqrt{32}\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}{\sqrt{32-32{{\sin }^{2}}\theta }\cos \theta d\theta } \\\ & =\sqrt{32}\times \sqrt{32}\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}{\sqrt{1-{{\sin }^{2}}\theta }\cos \theta d\theta }=32\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}{\cos \theta \times \cos \theta d\theta }=32\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}{{{\cos }^{2}}\theta d\theta } \\\ \end{aligned}$
Using the relation, ${{\cos }^{2}}\theta =\dfrac{1+\cos 2\theta }{2}$ we get
$32\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}{\dfrac{1+\cos 2\theta }{2}d\theta }$
We know the integration formula $\int{\cos n\theta d\theta =\dfrac{\sin n\theta }{n}}$. Using this formula, we get

& Area=32\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}{\dfrac{1+\cos 2\theta }{2}d\theta }=32\left[ \dfrac{\theta }{2}+\dfrac{\sin 2\theta }{4} \right]_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}=32\left[ \left( \dfrac{\dfrac{\pi }{2}}{2}+\dfrac{\sin 2\dfrac{\pi }{2}}{4} \right)-\left( \dfrac{\dfrac{\pi }{4}}{2}+\dfrac{\sin 2\dfrac{\pi }{4}}{4} \right) \right] \\\ & =32\left[ \dfrac{\pi }{4}-\dfrac{\pi }{8}-\dfrac{1}{4} \right]=32\left( \dfrac{\pi }{8}-\dfrac{1}{4} \right)=4\pi -8 \\\ \end{aligned}$$ Total area = $4\pi -8+8=4\pi$ **$\therefore $ The total area of the region is $4\pi $ sq. units.** **Note:** An alternative way to solve the problem is by calculating the area as area of the sector. The required area is the area of the sector in the circle. The included angle is $\dfrac{\pi }{4}$ as the line y = x makes an angle of $\dfrac{\pi }{4}$ with y = 0. The area of the sector with radius r units and included angle $\theta $ is given by $\dfrac{\theta }{360}\times \pi {{r}^{2}}$ Using this, here $r=\sqrt{32}$ and $\theta =4{{5}^{\circ }}$, we get area = $\dfrac{45}{360}\times \pi {{\left( \sqrt{32} \right)}^{2}}=\dfrac{1}{8}\pi \times 32=4\pi $