Question

Find the area of the region bounded by ${{y}^{2}}=9x$, x=4 and x=2 and the x-axis in the first quadrant.
(a) $16-2\sqrt{3}$
(b) $14-\sqrt{2}$
(c) $16-4\sqrt{2}$
(d) none of these

Answer 1

First, by graphically drawing the curve whose area is required and the fourth equation which is as x-axis is y=0. Then, we have marked the area ABCD which is the required curve cutting each other to get the desired area of the graph. Then, by using the area A of the curve by using the integral from limits 2 to 4.

Complete step-by-step answer:
In this question, we are supposed to find the area of the region bounded by ${{y}^{2}}=9x$, x=4 and x=2 and the x-axis in the first quadrant.
So, by graphically drawing the curve whose area is required as:

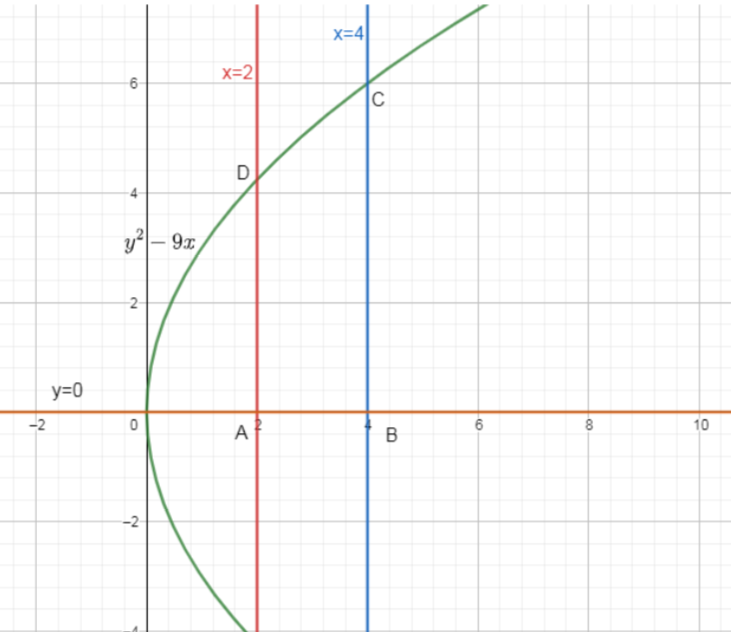
Now, the fourth equation which is as x-axis is y=0.
Then, we have marked the area ABCD which is the required curve cutting each other to get the desired area of the graph.
So, we can clearly see from the graph that y is varying from the value 2 to 4.
Now, by using the value of the equation given in the question as:
${{y}^{2}}=9x$
Now, by using the transformation to get the value of y in terms of x as:
$\begin{aligned} & y=\sqrt{9x} \\\ & \Rightarrow y=3\sqrt{x} \\\ \end{aligned}$
Then, by using the area A of the curve by using the integral from limits 2 to 4 as:
$A=\int\limits_{2}^{4}{ydx}$
Now, by substituting the value of y as $y=3\sqrt{x}$
$A=\int\limits_{2}^{4}{3\sqrt{x}dx}$
So, by solving the above integral to get the desired area as:
$A=3\left[\dfrac{ {{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right]_{2}^{4}$
$\Rightarrow A= 3 \times \dfrac{2}{3} \left[{4}^{\dfrac{3}{2}} - {2}^{\dfrac{3}{2}} \right]$
Now, by using the values of 2 and 4 to get the integral value as:
$\begin{aligned} & A=2\left( 8-2\sqrt{2} \right) \\\ & \Rightarrow A=16-4\sqrt{2} \\\ \end{aligned}$
So, the area between the curve is $16-4\sqrt{2}$.
Hence, option (c) is correct.

Note: Now, to solve these types of questions we need to know how to use the graphs to get the area of the figure which is cut by different lines as x=2 and x=4. Moreover, there is a condition that takes x-axis that means y=0 and by mistake we will not take it x=0.