Question
Question: Find the area of the region bounded by the parabola \[y={{x}^{2}}\] and \(y=\left| x \right|\)? 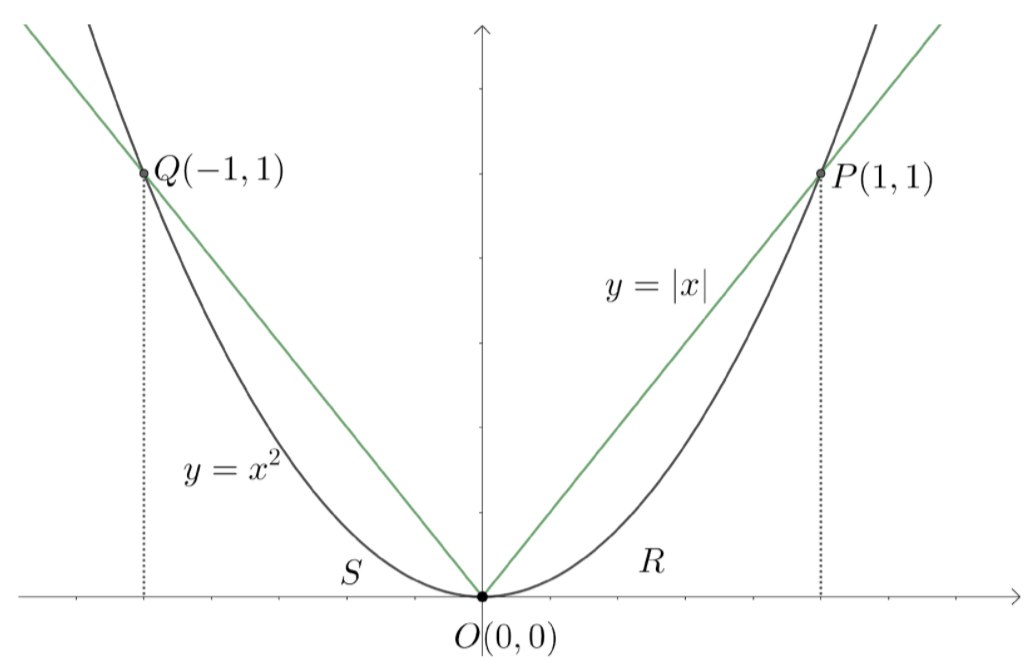
Solution
We start solving the problem by recalling the concept of finding area through integration. We find the limits of integration and integrand for the area from the plot drawn between the given two functions. We then use the definition of modulus function \left| x \right|=\left\\{ \begin{matrix} x,\text{ for }x>0 \\\ 0,\text{ for }x=0 \\\ -x,\text{ for }x<0 \\\ \end{matrix} \right. and ∫xndx=n+1xn+1+C, a∫bf′(x)=[f(x)]ab=f(b)−f(a) to find the integration result. We then make subsequent calculations to get the value of required area.
Complete step-by-step solution:
According to the problem, we need to find the area of the region bounded by the parabola y=x2 and the function y=∣x∣.
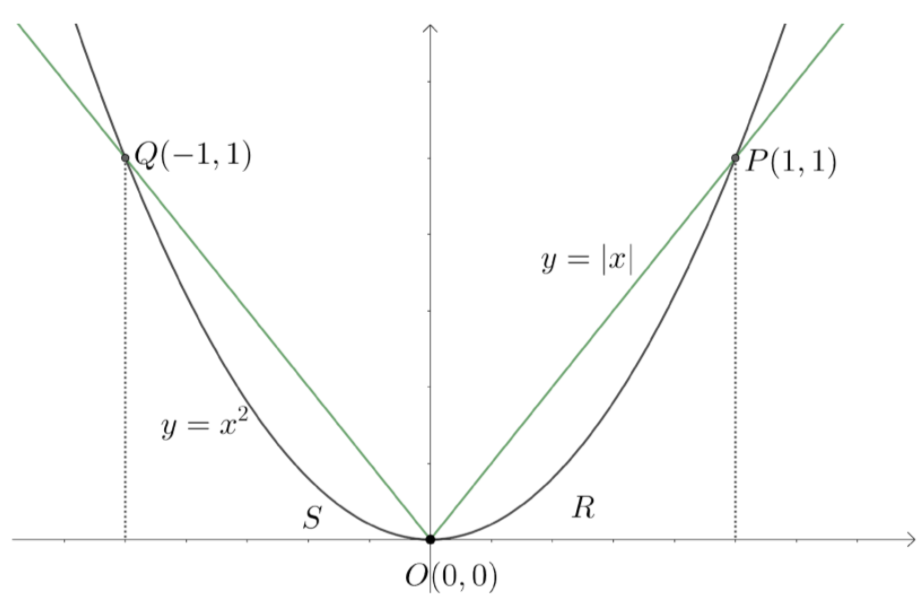
We know that the area bounded by the curves will be region where they were making a closed region. From the figure, we can see that the closed region formed by the region is between the points (−1,1) to (0,0) and between (0,0) and (1,1).
We know that the area bounded by the curves f(x), g(x) between the values x=a and x=bis defined by a∫bf(x)−g(x)dx, where aFromthefigurewecanseethatthefunctiony=\left| x \right|lies above the parabola $$y={{x}^{2}}$$ betweenx=-1andx=0,alsobetweenx=0andx=1.
So, the area of the region (A) bounded by the parabola $$y={{x}^{2}}$$ and the function y=\left| x \right|is,\Rightarrow A=\int\limits_{-1}^{0}{\left( \left| x \right|-{{x}^{2}} \right)dx}+\int\limits_{0}^{1}{\left( \left| x \right|-{{x}^{2}} \right)dx}−−−(1).Weknowthatthedefinitionofmodulusfunctionisdefinedas\left| x \right|=\left\{ \begin{matrix}
x,\text{ for }x>0 \\
0,\text{ for }x=0 \\
-x,\text{ for }x<0 \\
\end{matrix} \right..Weusethisinequation(1).\Rightarrow A=\int\limits_{-1}^{0}{\left( -x-{{x}^{2}} \right)dx}+\int\limits_{0}^{1}{\left( x-{{x}^{2}} \right)dx}.Weknowthat\int{\left( f\left( x \right)+g\left( x \right) \right)dx}=\int{f\left( x \right)dx}+\int{g\left( x \right)dx}.\Rightarrow A=\int\limits_{-1}^{0}{\left( -x \right)dx}+\int\limits_{0}^{1}{\left( -{{x}^{2}} \right)dx}+\int\limits_{0}^{1}{xdx}+\int\limits_{0}^{1}{\left( -{{x}^{2}} \right)dx}.\Rightarrow A=-\int\limits_{-1}^{0}{xdx}-\int\limits_{0}^{1}{{{x}^{2}}dx}+\int\limits_{0}^{1}{xdx}-\int\limits_{0}^{1}{{{x}^{2}}dx}.Weknowthat\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}+Cand\int\limits_{a}^{b}{{{f}^{'}}\left( x \right)}=\left[ f\left( x \right) \right]{a}^{b}=f\left( b \right)-f\left( a \right).\Rightarrow A=-\left[ \dfrac{{{x}^{2}}}{2} \right]{-1}^{0}-\left[ \dfrac{{{x}^{3}}}{3} \right]{-1}^{0}+\left[ \dfrac{{{x}^{2}}}{2} \right]{0}^{1}-\left[ \dfrac{{{x}^{3}}}{3} \right]_{0}^{1}.\Rightarrow A=-\left[ \dfrac{{{0}^{2}}}{2}-\dfrac{{{\left( -1 \right)}^{2}}}{2} \right]-\left[ \dfrac{{{0}^{3}}}{3}-\dfrac{{{\left( -1 \right)}^{3}}}{3} \right]+\left[ \dfrac{{{1}^{2}}}{2}-\dfrac{{{0}^{2}}}{2} \right]-\left[ \dfrac{{{1}^{3}}}{3}-\dfrac{{{0}^{3}}}{3} \right].\Rightarrow A=-\left[ \dfrac{0}{2}-\dfrac{1}{2} \right]-\left[ \dfrac{0}{3}-\left( \dfrac{-1}{3} \right) \right]+\left[ \dfrac{1}{2}-\dfrac{0}{2} \right]-\left[ \dfrac{1}{3}-\dfrac{0}{3} \right].\Rightarrow A=-\left[ 0-\dfrac{1}{2} \right]-\left[ 0+\dfrac{1}{3} \right]+\left[ \dfrac{1}{2}-0 \right]-\left[ \dfrac{1}{3}-0 \right].\Rightarrow A=-\left[ -\dfrac{1}{2} \right]-\left[ \dfrac{1}{3} \right]+\left[ \dfrac{1}{2} \right]-\left[ \dfrac{1}{3} \right].\Rightarrow A=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{2}-\dfrac{1}{3}.\Rightarrow A=\dfrac{1}{3}.
So, we have found the area bounded by the parabola $$y={{x}^{2}}$$ and the function y=\left| x \right|as\dfrac{1}{3}.
∴ The area bounded by the parabola $$y={{x}^{2}}$$ and the function y=\left| x \right|is\dfrac{1}{3}$.
Note: From the figure, we can see that the area bounded in the regions S and R are equal. So, we can find area of one region and multiply it with (2) in order to get the required area of the bounded. Whenever we are asked to find areas of two intersecting functions, we need to find the area of the closed bounded region. If those are not intersecting, limits of integration have to be given in order to get the area bounded between them.
