Question

Find the area of the region bounded by the parabola ${{y}^{2}}=4x$, the x-axis and the lines x=1 and x=4.

Answer 1

Hint: Plot the curve on the graph. Observe that the required area is the area in the first quadrant. For finding the area of the curve in the first quadrant express y in terms of x. Note that y>0 and hence take only the positive sign. Then use the fact that the area under the curve is given by $\int_{a}^{b}{ydx}$. Substitute suitable values of a and b and integrate and hence find the area.

Complete step-by-step answer:

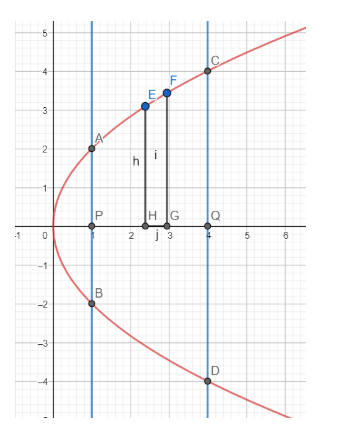
As is evident from the graph, the required area is the area in the first quadrant.
Now, we have ${{y}^{2}}=4x\Rightarrow y=\pm 2\sqrt{x}$
Since in the first quadrant, y is positive, we have $y=2\sqrt{x}$
Now consider the strip EFGH
We have EH = y and GH = dx
Hence the area of the strip is ydx.
The area in the first quadrant is the sum of the areas of the strips from P to Q.
Hence, we have
The area in the first quadrant $=\int_{1}^{4}{ydx}$
Substituting the value of y, we get
The area in the first quadrant $=\int_{1}^{4}{2\sqrt{x}dx}$
Let $I=\int_{1}^{4}{2\sqrt{x}dx}$
Now, we know that $\int_{a}^{b}{kf\left( x \right)dx}=k\int_{a}^{b}{f\left( x \right)dx}$
Hence, we have
$I=2\int_{1}^{4}{\sqrt{x}dx}$
Now, we know that $\int{{{x}^{n}}dx=\dfrac{{{x}^{n+1}}}{n+1},n\ne -1}$
Hence, we have
$I=2\left( \left. \dfrac{{{x}^{\dfrac{1}{2}+1}}}{\dfrac{1}{2}+1} \right|_{1}^{4} \right)=\left. \dfrac{4\times {{x}^{\dfrac{3}{2}}}}{3} \right|_{1}^{4}=4\times \left( \dfrac{{{4}^{\dfrac{3}{2}}}}{3}-\dfrac{{{1}^{\dfrac{3}{2}}}}{3} \right)=\dfrac{28}{3}$
Hence the area in the first quadrant is $\dfrac{28}{3}$ square units
Hence the area bounded by the curve ${{y}^{2}}=4x$, the x-axis and the ordinates x=1 and x= 4 is $\dfrac{28}{3}$ square units.

Note: Alternative solution:
Instead of taking vertical strips, we can take horizontal strips as shown

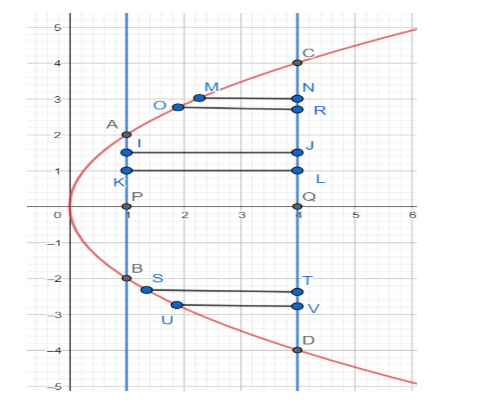
There are two types of horizontal strips
[1] MNRO (Lower bounded by $x=\dfrac{{{y}^{2}}}{4}$ and upper bounded by x=4)
[2] IJLK (Lower bounded by x=1 and upper bounded by x=4).
Area of the strip from C to A is $\left( 4-\dfrac{{{y}^{2}}}{4} \right)dy$
Area of the strip from A to P is $\left( 4-1 \right)dy$
Now, we have $A\equiv \left( 1,2 \right),B\equiv \left( 1,-2 \right),C\equiv \left( 4,4 \right)$ and $D\equiv \left( 4,-4 \right)$
Hence, we have

& A=\int_{0}^{2}{\left( 4-1 \right)dy}+\int_{2}^{4}{\left( 4-\dfrac{{{y}^{2}}}{4} \right)dy} \\\ & =6+8-\dfrac{56}{12}=14-\dfrac{14}{3}=\dfrac{28}{3} \\\ \end{aligned}$$ Hence the total area $=\dfrac{28}{3}$ square units, which is the same as obtained above.