Question
Question: Find the area of the region bounded by the curve \(y={{x}^{2}}\), the x-axis and the ordinates x = 1...
Find the area of the region bounded by the curve y=x2, the x-axis and the ordinates x = 1 and x= 3.
Solution
Hint: Plot the graph on a graph. Identify the region whose area is to be found. Use the fact that the area of the region bounded by y=f(x), the x-axis and the ordinates x = a and x= b is given by
y=∫ab∣f(x)∣dx. Hence argue that the required area is given by A=∫12x2dx. Integrate and hence find the required area.
Complete step-by-step answer:
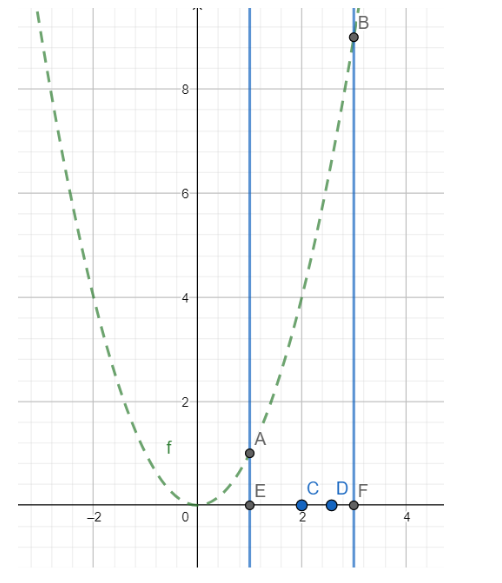
Hence the area bounded by the curve y=x2, the x-axis and the ordinates x= 1 and x= 2 is the area of the region AECDFBA.
We know that the area of the region bounded by y=f(x), the x-axis and the ordinates x = a and x= b is given by
y=∫ab∣f(x)∣dx.
Hence the required area =∫13x2dx
We know that ∀x∈R,x2=x2
Hence, we have
Required area =∫13x2dx
We know that ∫xndx=n+1xn+1 and according to the first fundamental theorem of calculus if F’(x) = f(x), then ∫abf(x)dx=F(b)−F(a)
Hence, we have
Required area =3x313=327−31=326
Hence the required area is 326 square units.
Note: Alternative Solution:
The area bounded by the curve y=xn, the x-axis and the ordinates x= a, and x= b, a,b≥0 is given by
n+1bn+1−an+1
Hence the required area =333−13=326 square units.
