Question

Find the area of the region bounded by the curve ${{y}^{2}}=4x$ and the line x=3

Answer 1

Hint: Plot the curve on a graph. Identify the region whose area is to be found. Observe that the region is symmetrical in the first and the fourth quadrants. Hence find the area in the first quadrant, and hence the area of the region will be two times the area in the first quadrant. For finding the area in the first curve quadrant express y in terms of x. Note that y>0 and hence take only the positive sign. Then use the fact that the area under the curve is given by $\int_{a}^{b}{ydx}$. Substitute suitable values of a and b and integrate and hence find the area.

Complete step-by-step answer:

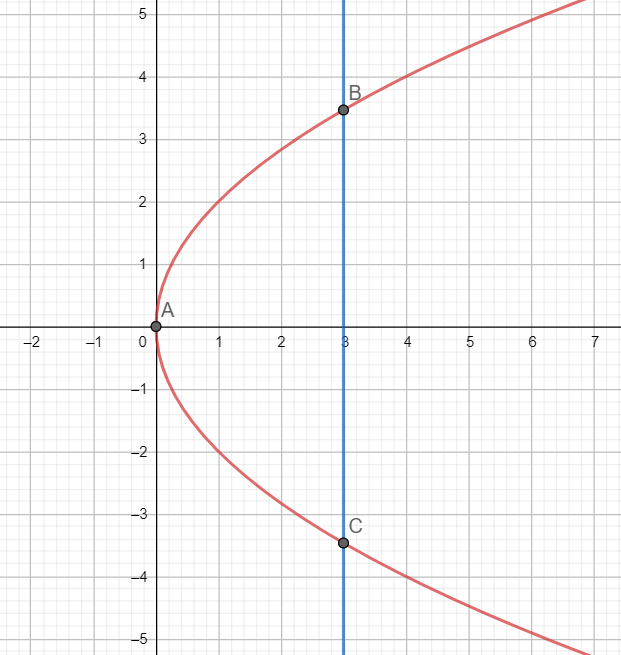
The region whose area is to be found is ABCA. As is evident from the graph that the region is symmetrical in the first and the fourth quadrants. Hence, we will find the area in the first quadrant, and then the total area will be two times the area in the first quadrant.
Now, we have
${{y}^{2}}=4x$
Hence, we have
$y=\pm 2\sqrt{x}$
Now since in the first quadrant, y>0.
Hence, we have
$y=2\sqrt{x}$

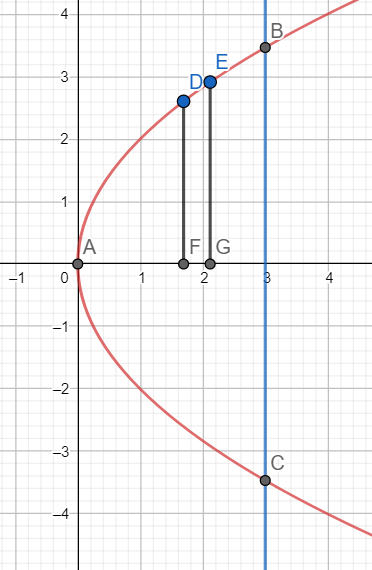
Now consider the vertical strip DEGF.
Here DF = y and FG = dx
Hence the area of the strip will be ydx.
The area in the first quadrant will be the sum of the area of these vertical strips from A to B.
Hence the area in the first quadrant will be $\int_{0}^{3}{ydx}$
Substituting the value of y, we get
The area in the first quadrant is $\int_{0}^{3}{2\sqrt{x}dx}$
Let $I=\int_{0}^{3}{2\sqrt{x}}$
We know that $\int_{a}^{b}{kf\left( x \right)dx}=k\int_{a}^{b}{f\left( x \right)dx}$
Hence, we have
$I=2\int_{0}^{3}{\sqrt{x}dx}$
Now, we know that $\int{{{x}^{n}}}=\dfrac{{{x}^{n+1}}}{n+1},n\ne -1$
Hence, we have
$I=2\left( \left. \dfrac{2}{3}{{x}^{\dfrac{3}{2}}} \right|_{0}^{3} \right)=\dfrac{4}{3}\left( 3\sqrt{3} \right)=4\sqrt{3}$
Hence the area in the first quadrant $=4\sqrt{3}$ square units
Hence the total area $=2\times 4\sqrt{3}=8\sqrt{3}$ square units.

Note: [1] Instead of taking vertical strips, we can take horizontal strips as shown below

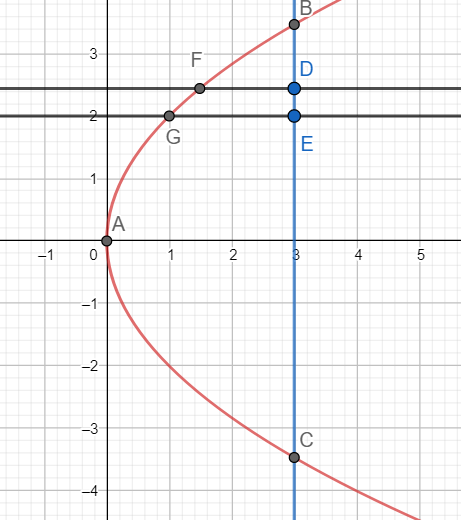
For the strip DEGF, we have
DE = dy and GE = $3-\dfrac{{{y}^{2}}}{4}$
Hence, we have
$A=\int_{-2\sqrt{3}}^{2\sqrt{3}}{\left( 3-\dfrac{{{y}^{2}}}{4} \right)dx}$
Since $\left( 3-\dfrac{{{y}^{2}}}{4} \right)$ is an even function, we have
$A=2\int_{0}^{2\sqrt{3}}{\left( 3-\dfrac{{{y}^{2}}}{4} \right)dy}=2\left( 6\sqrt{3}-\dfrac{24\sqrt{3}}{12} \right)=8\sqrt{3}$, which is the same as obtained above