Question

Find the area of the quadrilateral whose sides are 9 m, 40 m, 28 m, 15 m. The angle between the first two sides is ${90^ \circ }$.
A. 348 $m^2$
B. 315 $m^2$
C. 306 $m^2$
D. None of these

Answer 1

In the above question, we need to draw a diagonal in the quadrilateral which divides the quadrilateral into two triangles. In the first triangle, whose angle is ${90^ \circ }$ we will use the formula $\dfrac{1}{2} \times base \times height$. Then we will use the Pythagoras theorem to find the length of the diagonal. Then we will try to find the area of the second triangle by using the formula $\sqrt {s(s - a)(s - b)(s - c)}$. Then finally we will add the area of both the triangles to get the area of quadrilateral.

Complete step-by-step answer:
Let ABCD be a quadrilateral drawn in figure below.

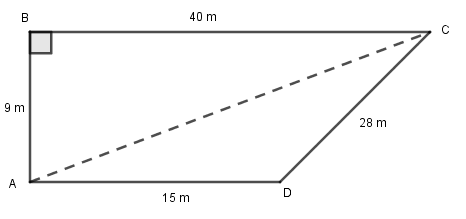
AB = 9 m, BC = 40 m, CD = 28 m, DA = 15 m and $\angle ABC = {90^ \circ }$
Area of quadrilateral ABCD = Area of $\vartriangle ABC$ + Area of $\vartriangle ACD$
In $\vartriangle ABC$, using the Pythagoras theorem,
$A{C^2} = A{B^2} + B{C^2}$
$\Rightarrow AC = \sqrt {{{\left( 9 \right)}^2} + {{\left( {40} \right)}^2}} = \sqrt {1681} = 41$m
Area of triangle ABC $= \dfrac{1}{2} \times AB \times BC$
$= \dfrac{1}{2} \times 9 \times 40 = 180 {m^2}$
Finding area of triangle ACD using heron’s formula
Area of triangle ACD $= \sqrt {s(s - a)(s - b)(s - c)}$
where $s = \dfrac{{a + b + c}}{2} = \dfrac{{15 + 28 + 41}}{2} = 42$m, a = 15 m, b = 28 m, c = 41 m.
Now putting the value of s in the above formula.
Area of triangle ACD $= \sqrt {42(42 - 15)(42 - 28)(42 - 41)}$
$= \sqrt {42 \times 27 \times 14 \times 1} = 126 {m^2}$
The area of quadrilateral ABCD = Area of triangle ABC + Area of triangle ACD
Thus, the area of quadrilateral ABCD = 180 + 126 = $306 {m^2}$

So, the correct answer is “Option C”.

Note: A method for calculating the area of a triangle when we have the length of all the three sides. Let a, b, c be the lengths of the sides of a triangle. Then Area $= \sqrt {s(s - a)(s - b)(s - c)}$ This formula is also known as Heron’s Formula.
Alternatively, you can use Heron’s formula for any type of triangle in which all sides are given, i.e. also for the right triangle.