Solveeit Logo
Login

Question

Question: Find the area of the polar curve,\(r = 2\sin \theta \) from \(0 \leqslant \theta \leqslant \pi .\)...

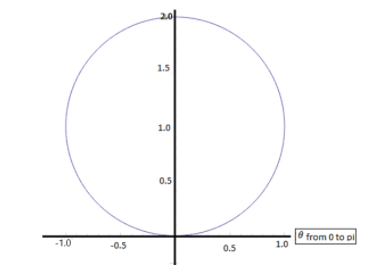
Find the area of the polar curve,r=2sin⁡θr = 2\sin \theta from 0⩽θ⩽π.0 \leqslant \theta \leqslant \pi .

Explanation

Solution

We’ll use the formula for the area of the polar curves which is A=∫θ1θ212r2dθA = \int\limits_{\theta 1}^{\theta 2} {\dfrac{1}{2}{r^2}d\theta } , using the integration method as the limits of the variable i.e. theta is given to us.
Substituting and then simplifying the equation we’ll get the area of the polar curves.

Complete step-by-step answer:
Given data: r=2sin⁡θr = 2\sin \theta where 0⩽θ⩽π.0 \leqslant \theta \leqslant \pi .

We know that the formula for the area of a polar curve is given by
A=∫θ1θ212r2dθA = \int\limits_{\theta 1}^{\theta 2} {\dfrac{1}{2}{r^2}d\theta }
Squaring both sides of the given curve
i.e. r=2sin⁡θr = 2\sin \theta
⇒r2=4sin⁡2θ\Rightarrow {r^2} = 4{\sin ^2}\theta
Therefore, the area of the given curve=∫0π12r2dθ= \int\limits_0^\pi {\dfrac{1}{2}{r^2}d\theta }
On Substituting the value of r, we get,
=∫0π4sin⁡2θ2dθ= \int\limits_0^\pi {\dfrac{{4{{\sin }^2}\theta }}{2}d\theta }
=∫0π2sin⁡2θdθ= \int\limits_0^\pi {2{{\sin }^2}\theta d\theta } ………..(1)
Using the double angle formula
i.e. cos⁡2x=1−2sin⁡2x\cos 2x = 1 - 2{\sin ^2}x
now, finding the value of sin⁡2x{\sin ^2}x
2sin⁡2x=1−cos⁡2x2{\sin ^2}x = 1 - \cos 2x
Dividing the equation by 2
sin⁡2x=12−cos⁡2x2{\sin ^2}x = \dfrac{1}{2} - \dfrac{{\cos 2x}}{2}
On substituting the value of sin⁡2x{\sin ^2}x in (1) we get,
=∫0π2(12−cos⁡2θ2)dθ= \int\limits_0^\pi {2\left( {\dfrac{1}{2} - \dfrac{{\cos 2\theta }}{2}} \right)d\theta }
On Simplifying the brackets, we get,
=∫0π(1−cos⁡2θ)dθ= \int\limits_0^\pi {(1 - \cos 2\theta )d\theta }
Now, using ∫αb(A+B)dx=∫αb(A)dx+∫αb(B)dx\int\limits_\alpha ^b {(A + B)dx} = \int\limits_\alpha ^b {(A)dx} + \int\limits_\alpha ^b {(B)dx} , we get,
=∫0π1dθ−∫0πcos⁡2θdθ= \int\limits_0^\pi {1d\theta } - \int\limits_0^\pi {\cos 2\theta d\theta }
Now using ∫αbxndx=∣xn+1n+1∣ab\int\limits_\alpha ^b {{x^n}dx} = \left| {\dfrac{{{x^{n + 1}}}}{{n + 1}}} \right|_a^band ∫αbcos⁡nxdx=∣sin⁡nx∣abn\int\limits_\alpha ^b {\cos nxdx} = \dfrac{{\left| {\sin nx} \right|_a^b}}{n}, we get,
=∣θ∣0π−∣sin⁡2θ∣0π2= \left| \theta \right|_0^\pi - \dfrac{{\left| {\sin 2\theta } \right|_0^\pi }}{2}
Now on simplifying the limits, we get,
=(π−0)−(sin⁡2π−sin⁡0)2= \left( {\pi - 0} \right) - \dfrac{{\left( {\sin 2\pi - \sin 0} \right)}}{2}
As, sin⁡2π=0\sin 2\pi = 0, we get,
=π= \pi
Hence, the area of the polar curve,r=2sin⁡θr = 2\sin \theta from 0⩽θ⩽π0 \leqslant \theta \leqslant \pi is π\pi .

Note: Most of the people just integrate r with the given limits of the variable
i.e. A=∫αbrdθA = \int\limits_\alpha ^b {rd\theta } , but this formula is wrong and won’t lead towards the correct answer, for any of the questions so avoid using this formula directly for the area of any of the polar curves.
Let simply using this formula,
Substituting the value of r and the limits
⇒A=∫0π2sin⁡θdθ\Rightarrow A = \int\limits_0^\pi {2\sin \theta d\theta }
Using ∫absin⁡xdx=∣−cos⁡x∣ab\int\limits_a^b {\sin xdx} = \left| { - \cos x} \right|_a^b
⇒A=∣−2cos⁡θ∣0π\Rightarrow A = \left| { - 2\cos \theta } \right|_0^\pi
Simplifying the limits
⇒A=−2(cos⁡π−cos⁡0)\Rightarrow A = - 2(\cos \pi - \cos 0)
Substituting the value of cos⁡π=−1\cos \pi = - 1and cos⁡0=1\cos 0 = 1
⇒A=4\Rightarrow A = 4
Therefore we can see as the results are not the same, hence this is the incorrect way to find the area of the polar curves so avoid using this formula.