Question
Question: Find the area of the polar curve, \(r=2\sin \theta \) from \(0\le \theta \le \pi \) ....
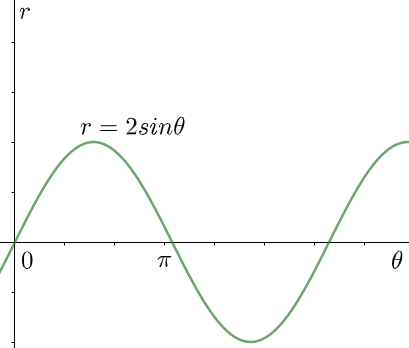
Find the area of the polar curve, r=2sinθ from 0≤θ≤π .
Solution
To find the area of the given curve, we need to integrate it with θ as variable from θ=0 to θ=π .
Complete step by step solution:
There are various coordinate systems. There are cartesian coordinate systems, polar coordinate systems and spherical coordinate systems. The cartesian coordinate system incorporates the x, y, and z coordinates. The polar coordinate incorporates the r, θ , z coordinates and the spherical coordinate incorporates the r, θ , ϕ . In a two-dimensional system, r- θ denotes the spherical coordinate system.
Finding the area under the curve, however, remains the same in any coordinate system, which is by integration within limits. In the cartesian coordinate system, we find the area under the curve y=f(x) by the help of the integration I=∫f(x)dx . Similarly, we find the area under the curve r=f(θ) by the help of the integration I=∫f(θ)dθ .
In this problem, the given curve that we have is r=2sinθ . To find the area under this curve, we need to integrate it within the limits θ=0 and θ=π . The integration thus is,
I=0∫π2sinθdθ⇒I=2[−cosθ]0π⇒I=2[−cosπ−(−cos0)]⇒I=2[1+1]⇒I=4
Therefore, we can conclude that the area of the given curve within θ=0 and θ=π is 4 .
Note: Finding area under a curve always means integrating it and nothing else. We should keep this in mind and should not get confused when we see any coordinate system other than the cartesian. We should also remember to apply the limits correctly.
