Question

Find the area of the greatest rectangle that can be inscribed in an ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$

Answer 1

We can assume a rectangle inside an ellipse now we know that general coordinates of any point is $(acos\theta ,bsin\theta )$ , so we consider 4 vertices of rectangles as $(acos\theta ,bsin\theta ), (acos\theta ,-bsin\theta ), (-acos\theta ,bsin\theta ) and (-acos\theta ,-bsin\theta )$
So side length of rectangle will be $2acos\theta$ and $2bsin\theta$ so its area will be $ab4sin\theta cos\theta$
Now we have to maximize area by differentiating and equating 0, and double differentiating and equating < 0.

Complete step-by-step solution:
We are given an ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ and a rectangle is inscribed in it so as we know general coordinates of any point in ellipse of equation $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ is $(acos\theta ,bsin\theta )$

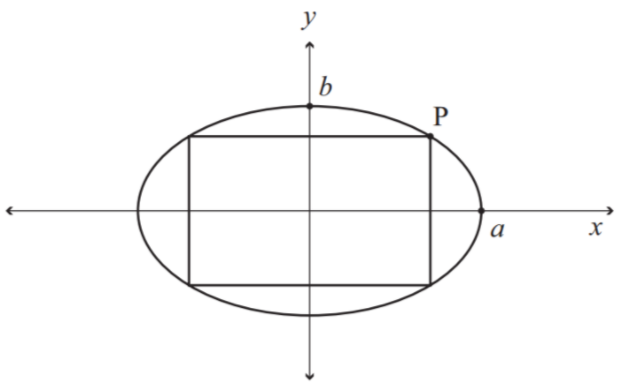
So, we take general vertices of rectangle as $(acos\theta, bsin\theta ), (acos\theta, -bsin\theta ), (-acos\theta, bsin\theta ) and (-acos\theta, -bsin\theta )$
So, we can see that length and breadth of rectangle is $2acos\theta$ and $2bsin\theta$
So, its area will be $ab4sin\theta cos\theta$ (length x Breadth)
Applying trigonometric formula $2sin\theta cos\theta =\sin 2\theta$, let area equals to A
Now $A=2ab\sin 2\theta$
Now as its the area is maximum given in question, we have to differentiate it with respect to $\theta$
$\dfrac{dA}{d\theta }=2ab\cos 2\theta \times 2$ (using $\dfrac{d\sin 2\theta }{d\theta }=2\cos 2\theta$)
Equating $\dfrac{dA}{d\theta }=2ab\cos 2\theta \times 2=0$, it means $\cos 2\theta =0$ , which means $2\theta =\dfrac{\pi }{2}$ and $\theta =\dfrac{\pi }{4}$
But we have to check that at $\theta =\dfrac{\pi }{4}$ area is maximum and not minimum
For that we have to calculate $\dfrac{{{d}^{2}}A}{d{{\theta }^{2}}}$
Which will be equals to $\dfrac{{{d}^{2}}A}{d{{\theta }^{2}}}=4ab(-\sin 2\theta )\times 2$
On solving further equals to $\dfrac{{{d}^{2}}A}{d{{\theta }^{2}}}=-8ab(\sin 2\theta )$ now putting $\theta =\dfrac{\pi }{4}$ we get
$\dfrac{{{d}^{2}}A}{d{{\theta }^{2}}}=-8ab$, which is a negative quantity hence we can say that area is maximum at $\theta =\dfrac{\pi }{4}$
So now we to put $\theta =\dfrac{\pi }{4}$ in equation of area which is $A=2ab\sin 2\theta$
We get as $A=2ab\sin 2\dfrac{\pi }{4}=2ab\sin \dfrac{\pi }{2}=2ab$
Hence max area of rectangle inside ellipse is $2ab$.

Note: If instead of ellipse we are given a circle ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ and to find area of the greatest rectangle that can be inscribed in it , again we can apply same procedure but this time the coordinates are $(rcos\theta ,rsin\theta ),(rcos\theta ,-rsin\theta ),(-rcos\theta ,rsin\theta )and(-rcos\theta ,-rsin\theta )$
So, we can see that length and breadth of the rectangle is $2rcos\theta$ and $2rsin\theta$. So, its area will be ${{r}^{2}}4sin\theta cos\theta$ (length x Breadth)
And after differentiating it results into $2{{r}^{2}}$